Problem Statement

Given an array of integer nums, check if there is a subarray of size K whose sum is equal to the target.

Example

Input:
nums = [9, 3, 2, 1, 8, 5, 6, 7, 2]
K = 4
target = 26

Output: true

Explanation: There is a subarray of size 4 [8, 5, 6, 7] whose sum is equal to 26.

Solution: Brute Force

Java Code

class Solution {
    private static boolean subarrayExists(int[] nums, int k, int target) {
        int n = nums.length;
        for(int i = 0; i < n - k + 1; i++) {
            int subarraySum = 0;
            for(int j = i; j < i + k; j++) {
                subarraySum += nums[j];
            }
            if(subarraySum == target) {
                return true;
            }
        }    
        return false;
    }
    
    public static void main(String[] args) {
        int[] nums = new int[]{9, 3, 2, 1, 8, 5, 6, 7, 2};
        int k = 4;
        int target = 26;
        System.out.println(subarrayExists(nums, k, target));
    }
}

C++ Code

#include <vector>
#include <iostream>
using namespace std;

class Solution {
public:
    static bool subarrayExists(vector<int> nums, int k, int target) {
        int n = nums.size();
        for (int i = 0; i <= n - k; i++) {
            int subarraySum = 0;
            for (int j = i; j < i + k; j++) {
                subarraySum += nums[j];
            }
            if (subarraySum == target) {
                return true;
            }
        }
        return false;
    }
};

int main() {
    vector<int> nums = {9, 3, 2, 1, 8, 5, 6, 7, 2};
    int k = 4;
    int target = 26;
    cout << (Solution::subarrayExists(nums, k, target) ? "True" : "False") << endl;
    return 0;
}

Python Code

class Solution:
    def subarrayExists(self, nums, k, target):
        n = len(nums)
        for i in range(n - k + 1): 
            subarray_sum = 0
            for j in range(i, i + k): 
                subarray_sum += nums[j]
            if subarray_sum == target: 
                return True
        return False 

nums = [9, 3, 2, 1, 8, 5, 6, 7, 2]
k = 4
target = 26
print(Solution().subarrayExists(nums, k, target))  

Complexity Analysis

Time Complexity: O(N * K), where N is the size of the array nums, and K is the size of the subarray.
Space Complexity: O(1)

Solution 2: Using Sliding Window

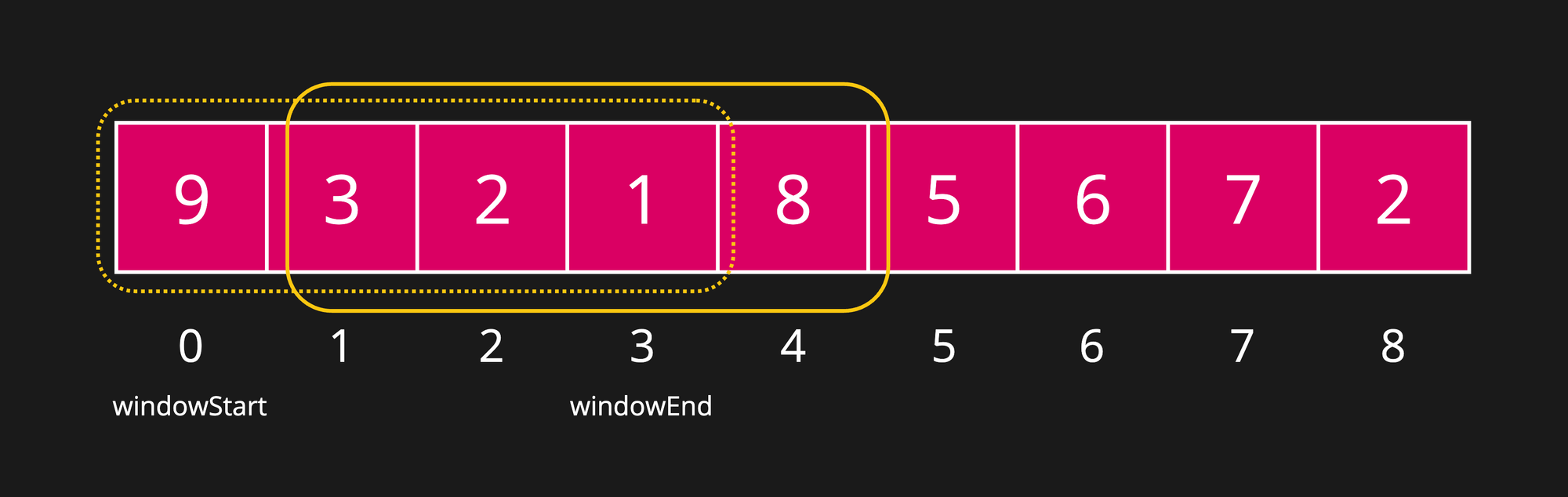
Java Code

class Solution {
    private static boolean subarrayExists(int[] nums, int k, int target) {
        int windowStart = 0;
        int windowSum = 0;
        
        for(int windowEnd = 0; windowEnd < n; windowEnd++) {
            windowSum += nums[windowEnd];
            if(windowEnd >= (k - 1)) {
                if(windowSum == target) {
                    return true;
                }
                windowSum -= nums[windowStart];
                windowStart += 1;
            }
        }
        return false;
    }
    public static void main(String[] args) {
        int[] nums = new int[]{9, 3, 2, 1, 8, 5, 6, 7, 2};
        int k = 4;
        int target = 26;
        
        System.out.println(subarrayExists(nums, k, target));
    }
}

C++ Code

#include <vector>
#include <iostream>
using namespace std;

class Solution {
public:
    static bool subarrayExists(vector<int>& nums, int k, int target) {
        int windowStart = 0, windowSum = 0;
        int n = nums.size();

        for (int windowEnd = 0; windowEnd < n; windowEnd++) {
            windowSum += nums[windowEnd];
            if (windowEnd >= k - 1) {  
                if (windowSum == target) {
                    return true;
                }
                windowSum -= nums[windowStart];
                windowStart++;
            }
        }
        return false;
    }
};

int main() {
    vector<int> nums = {9, 3, 2, 1, 8, 5, 6, 7, 2};
    int k = 4;
    int target = 26;
    
    cout << (Solution::subarrayExists(nums, k, target) ? "True" : "False") << endl;
    return 0;
}

Python Code

class Solution:
    def subarrayExists(self, nums, k, target):
        window_start = 0
        window_sum = 0
        n = len(nums)

        for window_end in range(n):
            window_sum += nums[window_end] 
            if window_end >= k - 1: 
                if window_sum == target:
                    return True
                window_sum -= nums[window_start] 
                window_start += 1

        return False

nums = [9, 3, 2, 1, 8, 5, 6, 7, 2]
k = 4
target = 26

print(Solution().subarrayExists(nums, k, target)) 

Complexity Analysis

Time Complexity: O(N), where N is the size of the array nums.
Space Complexity: O(1)