Number of Connected Components in an Undirected Graph - [LC Premium]
Problem Statement
You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.
Return the number of connected components in the graph.
Example 1
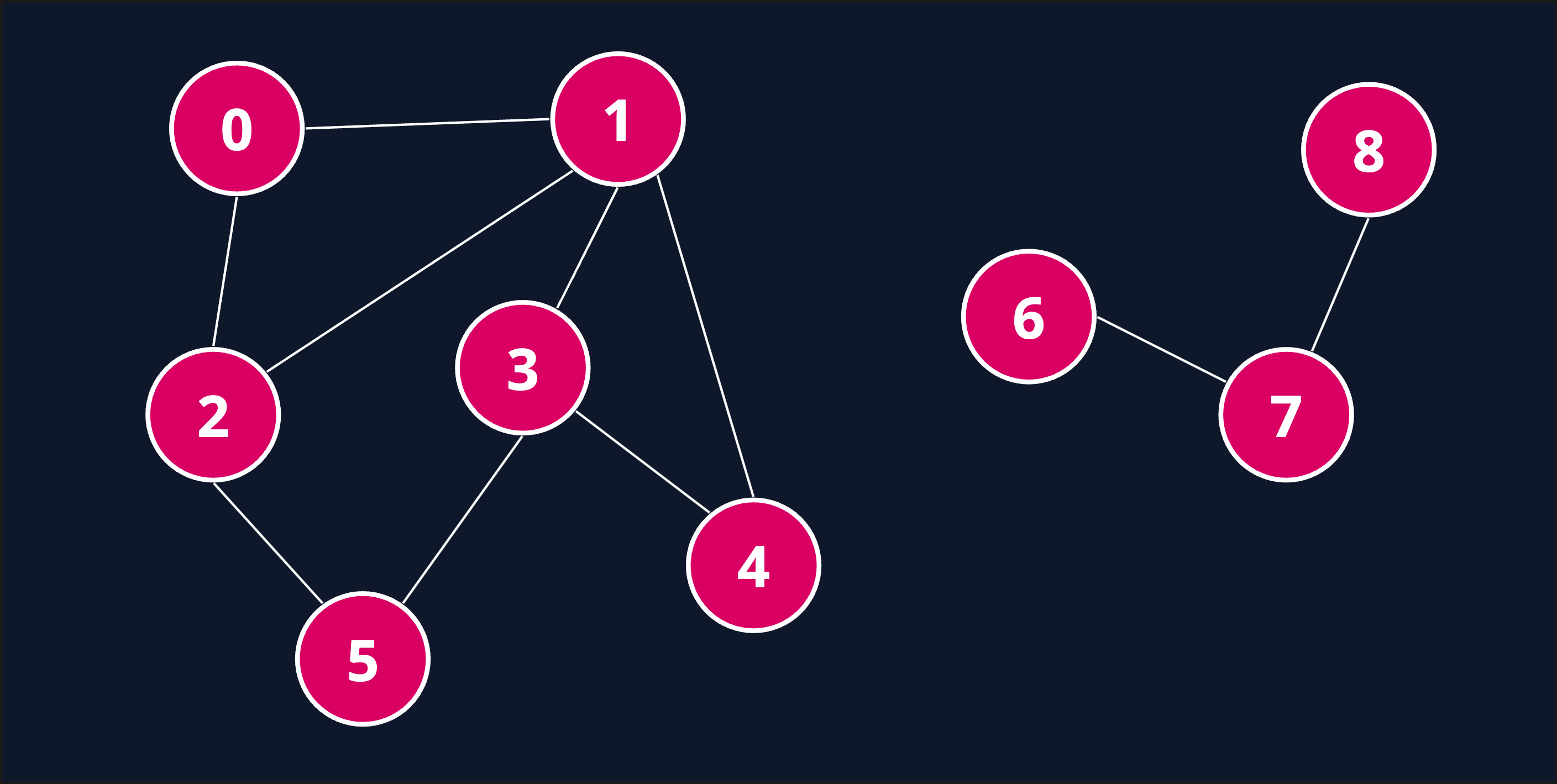
Input: n = 9, edges = [[0,1],[0,2],[1,2],[1,3],[1,4],[2,5],[3,4],[3,5],[6,7],[7,8]]
Output: 2
Example 2
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2
Try here before watching the video.
Video Solution
Java Code
import java.util.ArrayList;
import java.util.List;
class Solution {
public List<List<Integer>> buildGraph(int[][] edges, int n) {
List<List<Integer>> graph = new ArrayList<>();
for(int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
for(int[] edge : edges) {
graph.get(edge[0]).add(edge[1]);
graph.get(edge[1]).add(edge[0]);
}
return graph;
}
private void solve(int node, List<List<Integer>> graph, boolean[] visited) {
visited[node] = true;
for(int nbr : graph.get(node)) {
if(!visited[nbr]) {
solve(nbr, graph, visited);
}
}
}
public int countComponents(int n, int[][] edges) {
List<List<Integer>> graph = buildGraph(edges, n);
boolean[] visited = new boolean[n];
int count = 0;
for(int src = 0; src < n; src++) {
if(!visited[src]) {
solve(src, graph, visited);
count += 1;
}
}
return count;
}
}
C++ Code
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
vector<vector<int>> buildGraph(vector<vector<int>>& edges, int n) {
vector<vector<int>> graph(n);
for (const auto& edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
return graph;
}
void solve(int node, vector<vector<int>>& graph, vector<bool>& visited) {
visited[node] = true;
for (int nbr : graph[node]) {
if (!visited[nbr]) {
solve(nbr, graph, visited);
}
}
}
int countComponents(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph = buildGraph(edges, n);
vector<bool> visited(n, false);
int count = 0;
for(int src = 0; src < n; src++) {
if(!visited[src]) {
solve(src, graph, visited);
count += 1;
}
}
return count;
}
};
Python Code
class Solution:
def build_graph(self, edges, n):
graph = []
for i in range(n):
graph.append(list())
for edge in edges:
graph[edge[0]].append(edge[1])
graph[edge[1]].append(edge[0])
return graph
def solve(self, node, graph, visited):
visited[node] = True
for nbr in graph[node]:
if not visited[nbr]:
self.solve(nbr, graph, visited)
def countComponents(self, n: int, edges: List[List[int]]) -> int:
graph = self.build_graph(edges, n)
visited = [False] * n
count = 0
for src in range(n):
if visited[src] is not True:
self.solve(src, graph, visited)
count += 1
return count
Javascript Code
var countComponents = function(n, edges) {
function buildGraph(edges, n) {
const graph = new Array(n).fill(null).map(() => []);
for (const edge of edges) {
graph[edge[0]].push(edge[1]);
graph[edge[1]].push(edge[0]);
}
return graph;
}
function solve(node, graph, visited) {
visited[node] = true;
for (const nbr of graph[node]) {
if (!visited[nbr]) {
solve(nbr, graph, visited);
}
}
}
const graph = buildGraph(edges, n);
const visited = new Array(n).fill(false);
let count = 0;
for (let src = 0; src < n; src++) {
if (!visited[src]) {
solve(src, graph, visited);
count += 1;
}
}
return count;
};
Go Code
func countComponents(n int, edges [][]int) int {
graph := buildGraph(edges, n)
visited := make([]bool, n)
count := 0
for src := 0; src < n; src++ {
if !visited[src] {
solve(src, graph, visited)
count += 1
}
}
return count
}
func buildGraph(edges [][]int, n int) [][]int {
graph := make([][]int, n)
for i := 0; i < n; i++ {
graph[i] = make([]int, 0)
}
for _, edge := range edges {
graph[edge[0]] = append(graph[edge[0]], edge[1])
graph[edge[1]] = append(graph[edge[1]], edge[0])
}
return graph
}
func solve(node int, graph [][]int, visited []bool) {
visited[node] = true
for _, nbr := range graph[node] {
if !visited[nbr] {
solve(nbr, graph, visited)
}
}
}
Complexity Analysis
Time Complexity: O(V + E), where V is the total number of vertices and E is the number of edges.
Space Complexity: O(V + E), where V is the total number of vertices and E is the number of edges.