Skip to main content

Breadth First Search

How to traverse on Matrix in Graph?

Video Explanation

While solving problems on the Breadth First Search technique, you will find so many problems on a matrix where you would need to apply the BFS or DFS technique. Therefore, it's important to understand how we can traverse on matrix.

Let's recall what do we need to apply BFS on a Graph using Adjacency List.

  • Queue: to get the next element to be processed and for which we need to traverse its neighbors.
  • Visited: an array, so that we don't visit cells again if they are visited once.
  • That's it.
💡
In the case of a matrix, we may or may not need a visited array. The reason is simple. Suppose if, we visit a cell that contains 1 as a value. Therefore, we can change its value to some other value let's say 2. By doing this, we will come to know whether a cell is already visited or not. And hence, we might not require a separate visited array.

Now, the important thing is how to get the neighbors of any cell.

How to get neighbors?

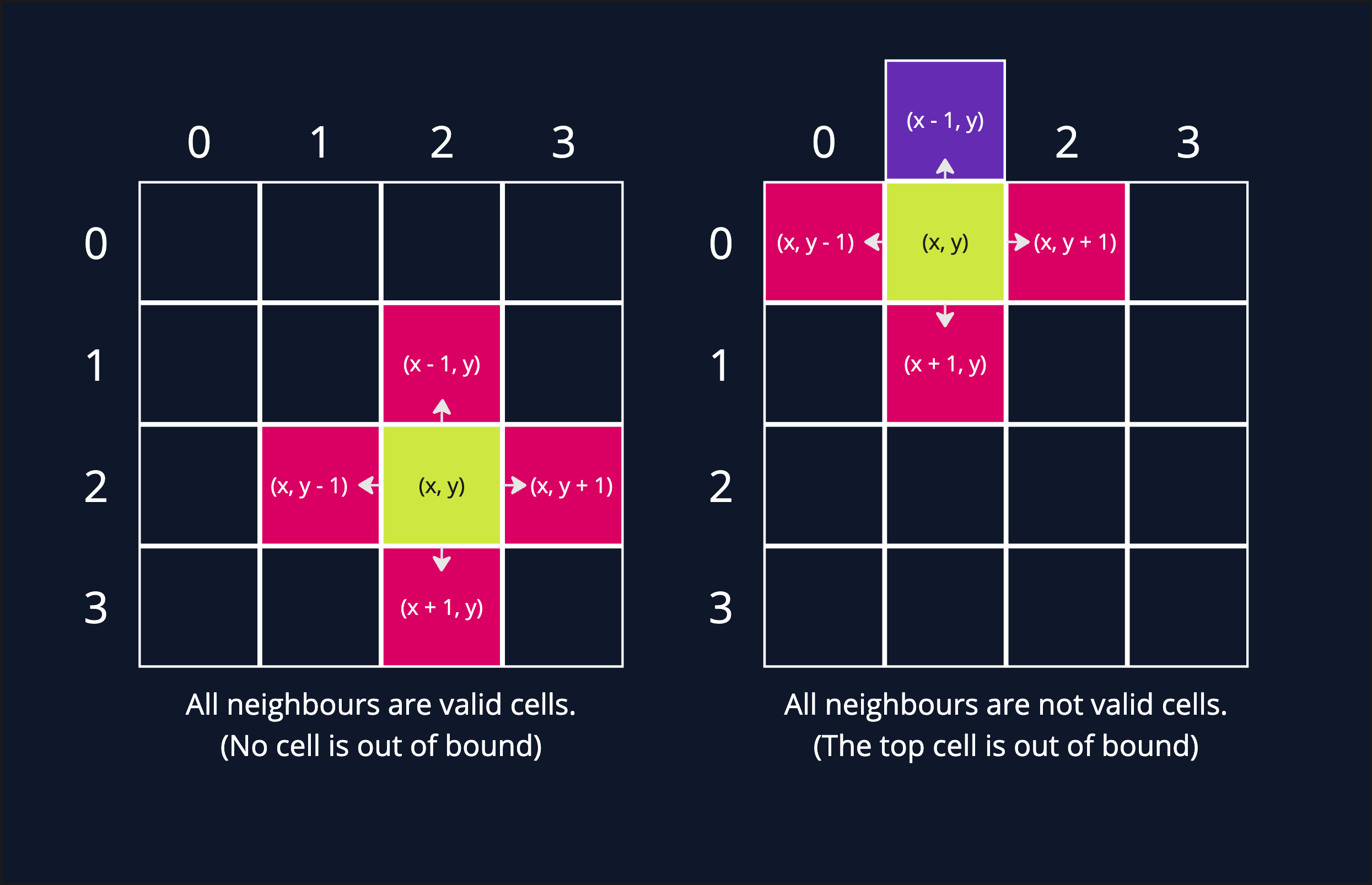
Let's suppose we are in any (x, y) cell and we want to get neighbors of this cell. Then the neighbor cells would be top, right, bottom, and left.

The neighbors are not always valid cells. How? Look at the right matrix below. The top cell is invalid. We cannot try to access this. Therefore, we need to make sure that we need to reach only valid cells otherwise, we will get Out of bound error.

The direction array

directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]

If we add these values to any (x, y) pair, we will get the required top, right, bottom, and left cells respectively.

Pseudocode

bfsOnMatrix(int[][] matrix) {
    rows = matrix.length
    cols = matrix[0].length
    
    queue = Queue()
    queue.add([0, 0]);
    // matrix[0][0] = 1000, assign any integer so that we can know whether it's visited or not.
    
    while(!queue.isEmpty()) {
        x, y = queue.pop()
        for(direction in directions) {
            newX = x + direction[0]
            newY = y + direction[1]
            if(isValidCell(newX, newY, rows, cols)) {
                queue.add([newX, newY]);
                // matrix[newX][newY] = 1000, assign any integer so that we can know whether it's visited or not.
            }
        }
    }
}

How to check for valid cells?

boolean isValidCell(int x, int y, int rows, int cols) {
    return (x >= 0 && x < rows && y >= 0 && y < cols);
}

We hope you have understood the basic concept of matrix. Things will fall into place when we will solve some questions. Next chapter onwards, we will start solving problems.