Max Area of Island
Problem Statement
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1
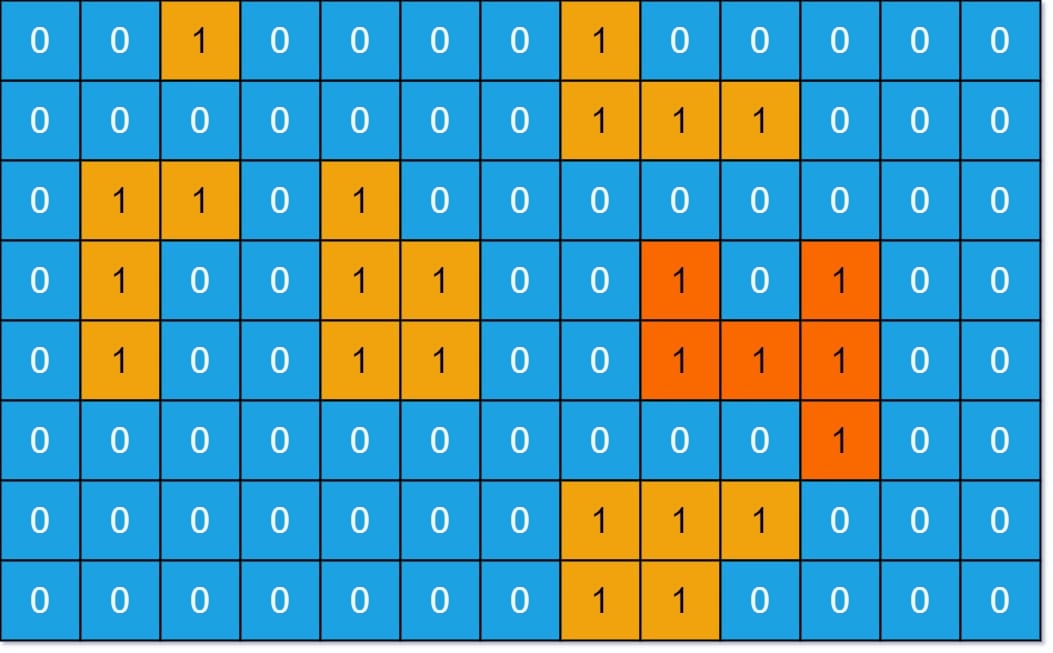
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.
Example 2
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0
Video Explanation: Coming Soon
Java Code
class Solution {
int[][] directions = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private int dfs(int row, int col, int[][] grid) {
if(row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] != 1) {
return 0;
}
int count = 1;
grid[row][col] = 2;
for(int[] direction : directions) {
int new_row = row + direction[0];
int new_col = col + direction[1];
count += dfs(new_row, new_col, grid);
}
return count;
}
public int maxAreaOfIsland(int[][] grid) {
int maxCount = 0;
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(grid[i][j] == 1) {
int count = dfs(i, j, grid);
maxCount = Math.max(maxCount, count);
}
}
}
return maxCount;
}
}
C++ Code
class Solution {
public:
vector<vector<int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int dfs(int row, int col, vector<vector<int>>& grid) {
if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() || grid[row][col] != 1) {
return 0;
}
int count = 1;
grid[row][col] = 2;
for (vector<int>& direction : directions) {
int new_row = row + direction[0];
int new_col = col + direction[1];
count += dfs(new_row, new_col, grid);
}
return count;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int maxCount = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == 1) {
int count = dfs(i, j, grid);
maxCount = max(maxCount, count);
}
}
}
return maxCount;
}
};
Python Code
class Solution:
directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]
def dfs(self, row, col, grid):
if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]) or grid[row][col] != 1:
return 0
count = 1
grid[row][col] = 2
for direction in self.directions:
new_row, new_col = row + direction[0], col + direction[1]
count += self.dfs(new_row, new_col, grid)
return count
def maxAreaOfIsland(self, grid):
maxCount = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
count = self.dfs(i, j, grid)
maxCount = max(maxCount, count)
return maxCount
Javascript Code
var maxAreaOfIsland = function(grid) {
const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];
function dfs(row, col) {
if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] !== 1) {
return 0;
}
let count = 1;
grid[row][col] = 2;
for (const direction of directions) {
const new_row = row + direction[0];
const new_col = col + direction[1];
count += dfs(new_row, new_col);
}
return count;
}
let maxCount = 0;
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === 1) {
const count = dfs(i, j);
maxCount = Math.max(maxCount, count);
}
}
}
return maxCount;
};
Go Code
package main
func maxAreaOfIsland(grid [][]int) int {
directions := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
var dfs func(row, col int) int
dfs = func(row, col int) int {
if row < 0 || row >= len(grid) || col < 0 || col >= len(grid[0]) || grid[row][col] != 1 {
return 0
}
count := 1
grid[row][col] = 2
for _, direction := range directions {
new_row, new_col := row+direction[0], col+direction[1]
count += dfs(new_row, new_col)
}
return count
}
maxCount := 0
for i := 0; i < len(grid); i++ {
for j := 0; j < len(grid[0]); j++ {
if grid[i][j] == 1 {
count := dfs(i, j)
maxCount = max(maxCount, count)
}
}
}
return maxCount
}
Complexity Analysis
Time Complexity: O(m * n), where m is the number of rows and n is the number of columns in the grid.
Space Complexity: O(m * n), where m is the number of rows and n is the number of columns in the grid.