Breadth-First Search - Graph Algorithm
Problem Statement
You are given a set of edges, n, and src, where edges represents the connection between two nodes, n represents the number of nodes, and src represents the source node. Traverse the entire graph in a breadth-first fashion.
Example
Input:
edges = [[0, 1], [0, 2], [1, 2], [1, 3], [1, 4], [2, 5], [3, 4], [3, 5]]
n = 6
src = 0
Output:
0 1 2 3 4 5
Video Solution
Breadth-First Search
The Breadth First Search (BFS) is an algorithm for traversing or searching tree or graph data structures. It explores all the nodes at the present level before moving on to the nodes at the next level.
Algorithm
Here are the steps for the BFS algorithm:
- Initialize a
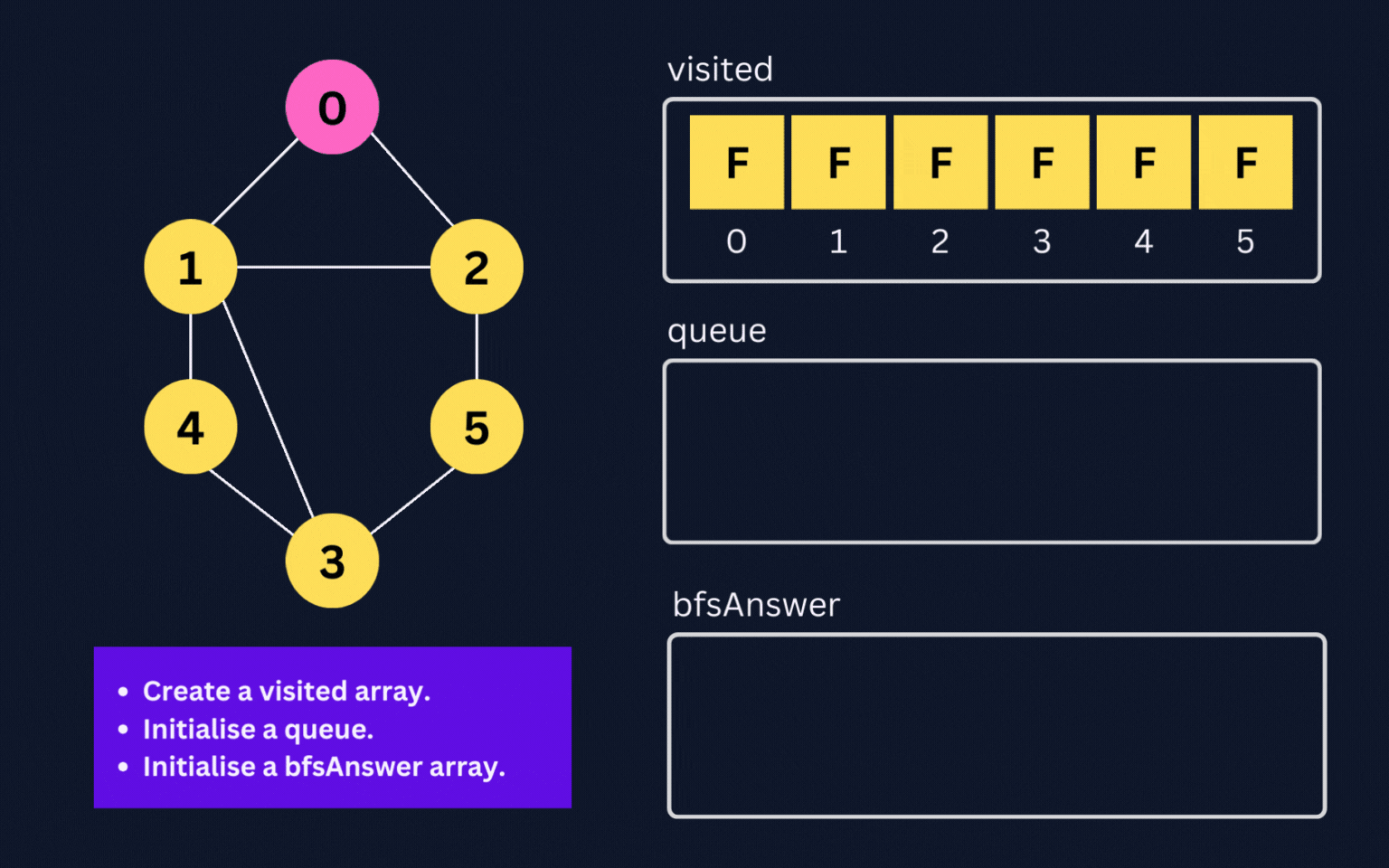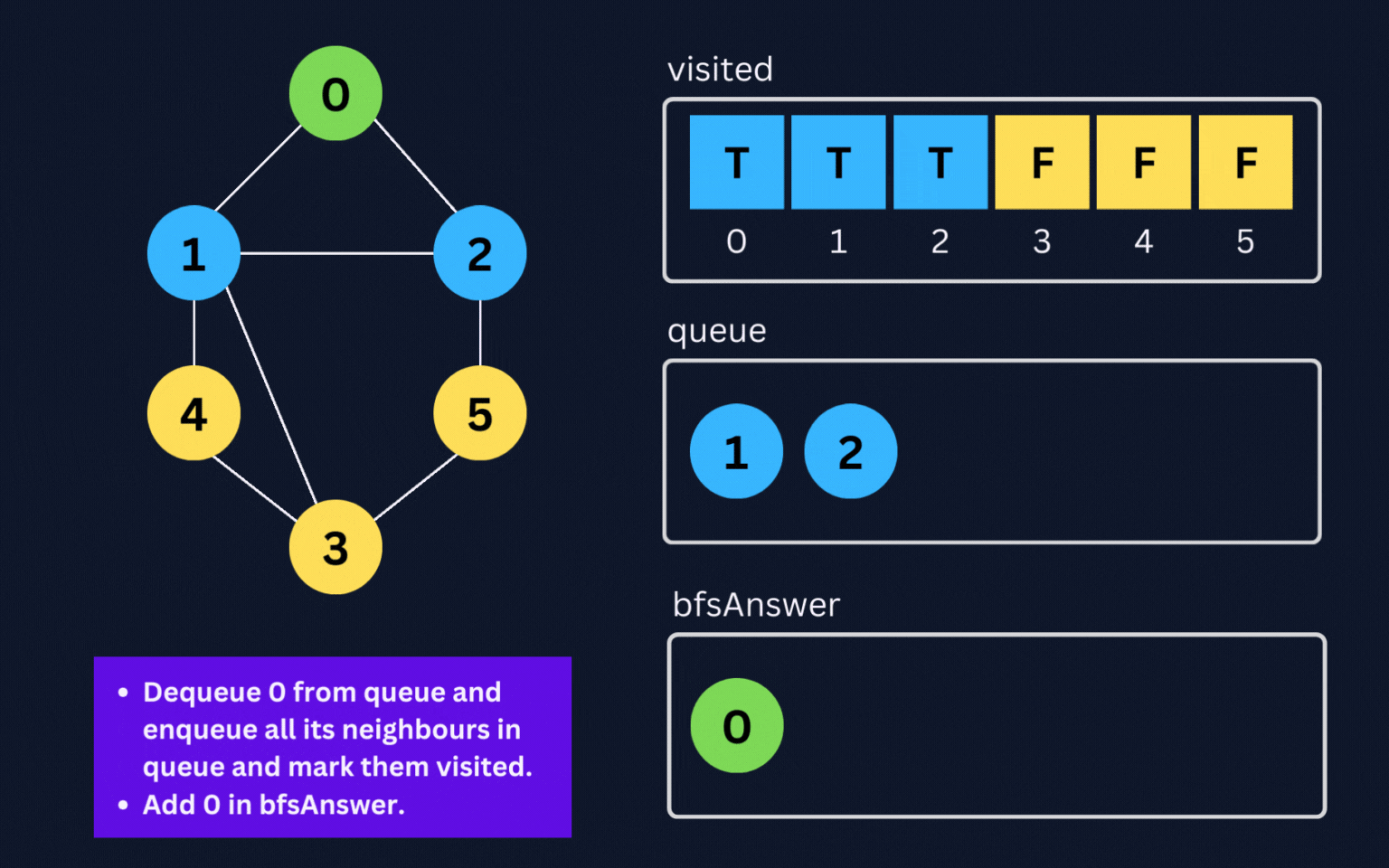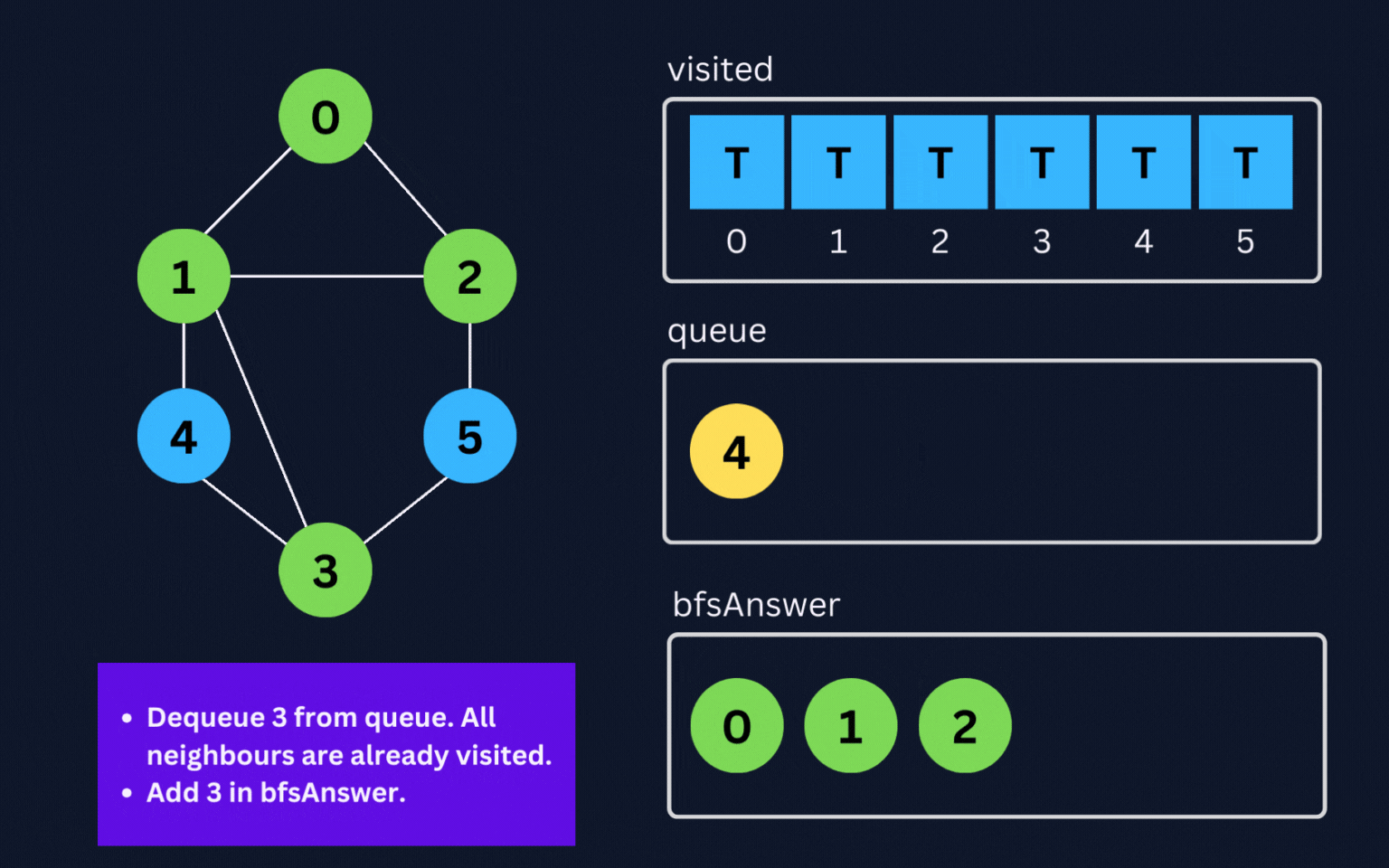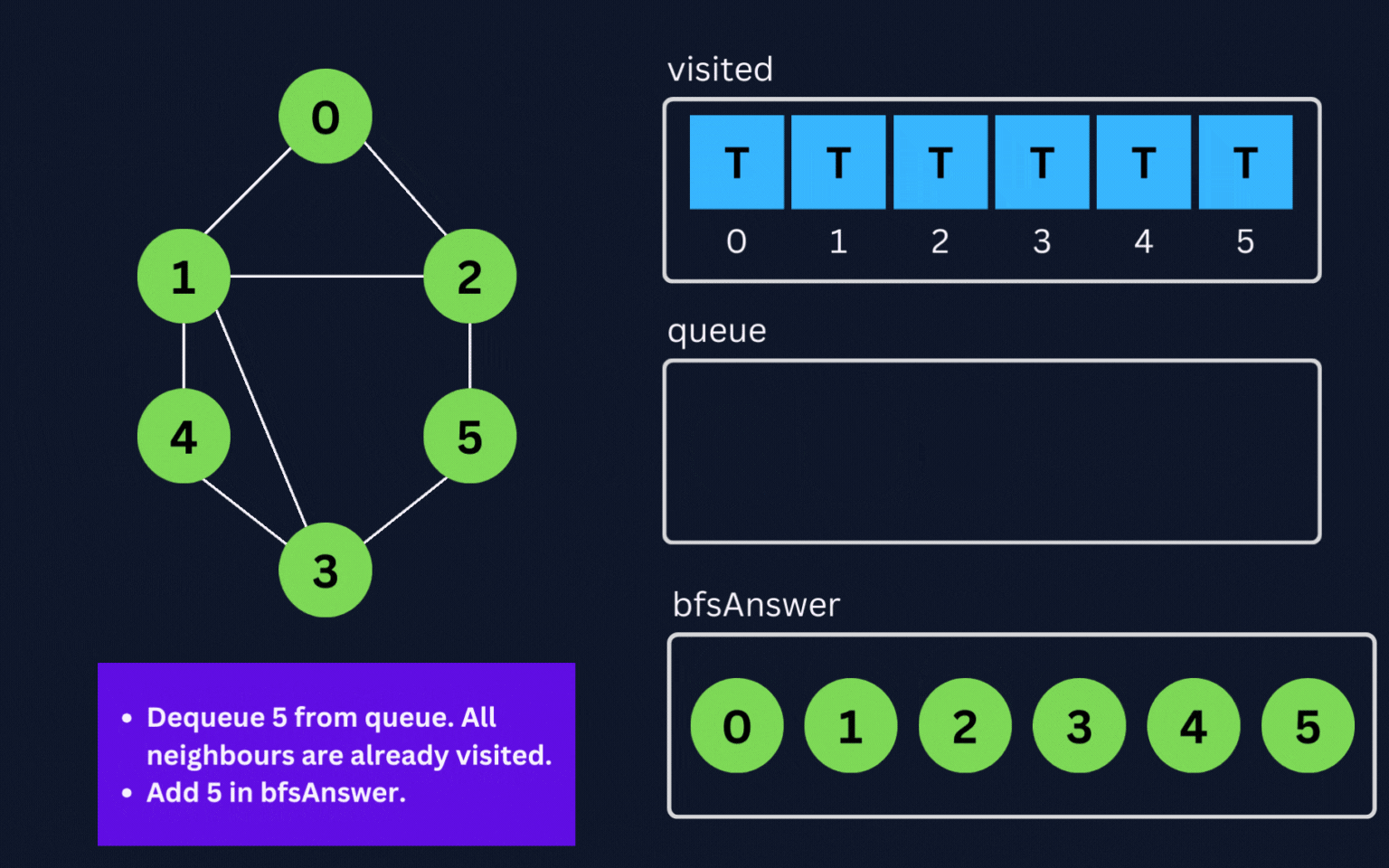
queue, abfsAnswerarray/list, and avisitedarray. - Pick a source node let's say
src, enqueue it, and mark it as visited by settingvisited[src] = true;. - Start a while loop and do the following:
- Dequeue an element from
queuelet's saycurr. - Add it to
bfsAnswerand enqueue all its adjacent nodes into a queue (if they are not visited) and mark them visited. - Repeat this process until the queue is empty.
- Dequeue an element from
The program can be stuck in an infinite loop if a node is revisited and was not marked as visited before. Hence, prevent exploring nodes that are visited by marking them as visited. And this is why visited array is important.
Visualization
Java Code
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
class BreadthFirstSearch {
public List<List<Integer>> buildGraph(int[][] edges, int n) {
List<List<Integer>> graph = new ArrayList<>();
for(int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
for(int[] edge : edges) {
graph.get(edge[0]).add(edge[1]);
graph.get(edge[1]).add(edge[0]);
}
return graph;
}
private int[] breadthFirstSearch(int[][] edges, int n, int src) {
List<List<Integer>> graph = buildGraph(edges, n);
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[n];
int[] bfsAnswer = new int[n];
queue.add(src);
visited[src] = true;
int index = 0;
while(!queue.isEmpty()) {
int curr = queue.poll();
bfsAnswer[index++] = curr;
for(int nbr : graph.get(curr)) {
if(!visited[nbr]) {
queue.add(nbr);
visited[nbr] = true;
}
}
}
return bfsAnswer;
}
public static void main(String[] args) {
int[][] edges = new int[][]{{0, 1}, {0, 2}, {1, 2}, {1, 3}, {1, 4}, {2, 5}, {3, 4}, {3, 5}};
int n = 6;
int src = 0;
BreadthFirstSearch bfs = new BreadthFirstSearch();
int[] bfsAnswer = bfs.breadthFirstSearch(edges, n, src);
for(int node : bfsAnswer) {
System.out.println(node + " ");
}
}
}
C++ Code
#include<bits/stdc++.h>
using namespace std;
class BreadthFirstSearch {
public:
vector<vector<int>> buildGraph(vector<vector<int>> &edges, int n) {
vector<vector<int>> graph;
for(int i = 0; i < n; i++) {
vector<int> nbrs;
graph.push_back(nbrs);
}
for(auto &edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
return graph;
}
vector<int> breadthFirstSearch(vector<vector<int>> &edges, int n, int src) {
vector<vector<int>> graph = buildGraph(edges, n);
queue<int> q;
vector<bool> visited(n, false);
vector<int> bfsAnswer;
q.push(src);
visited[src] = true;
while(!q.empty()) {
int curr = q.front();
q.pop();
bfsAnswer.push_back(curr);
for(auto &nbr : graph[curr]) {
if(!visited[nbr]) {
q.push(nbr);
visited[nbr] = true;
}
}
}
return bfsAnswer;
}
};
int main(int argc, char const *argv[]) {
vector<vector<int>> edges = {{0, 1}, {0, 2}, {1, 2}, {1, 3}, {1, 4}, {2, 5}, {3, 4}, {3, 5}};
int n = 6;
int src = 0;
BreadthFirstSearch bfs;
vector<int> bfsAnswer = bfs.breadthFirstSearch(edges, n, src);
for(auto node : bfsAnswer) {
cout << node << " ";
}
}
Python Code
from collections import deque
class BreadthFirstSearch:
def build_graph(self, edges, n):
graph = []
for i in range(n):
graph.append(list())
for edge in edges:
graph[edge[0]].append(edge[1])
graph[edge[1]].append(edge[0])
return graph
def breadth_first_search(self, edges, n, src):
graph = self.build_graph(edges, n)
queue = deque()
visited = [False] * n
bfs_answer = []
queue.append(src)
visited[src] = True
while queue:
curr = queue.popleft()
bfs_answer.append(curr)
for nbr in graph[curr]:
if visited[nbr] is not True:
queue.append(nbr)
visited[nbr] = True
return bfs_answer
if __name__ == '__main__':
edges = [[0, 1], [0, 2], [1, 2], [1, 3], [1, 4], [2, 5], [3, 4], [3, 5]]
n = 6
src = 0
bfs = BreadthFirstSearch()
bfs_answer = bfs.breadth_first_search(edges, n, src)
for node in bfs_answer:
print(node, end = " ")
Javascript Code
class BreadthFirstSearch {
buildGraph(edges, n) {
const graph = Array.from({ length: n }, () => []);
for (const edge of edges) {
graph[edge[0]].push(edge[1]);
graph[edge[1]].push(edge[0]);
}
return graph;
}
breadthFirstSearch(edges, n, src) {
const graph = this.buildGraph(edges, n);
const queue = [];
const visited = new Array(n).fill(false);
const bfsAnswer = [];
queue.push(src);
visited[src] = true;
let index = 0;
while (queue.length !== 0) {
const curr = queue.shift();
bfsAnswer[index++] = curr;
for (const nbr of graph[curr]) {
if (!visited[nbr]) {
queue.push(nbr);
visited[nbr] = true;
}
}
}
return bfsAnswer;
}
}
const edges = [
[0, 1], [0, 2],
[1, 2], [1, 3],
[1, 4], [2, 5],
[3, 4], [3, 5]
];
const n = 6;
const src = 0;
const bfs = new BreadthFirstSearch();
const bfsAnswer = bfs.breadthFirstSearch(edges, n, src);
for (const node of bfsAnswer) {
process.stdout.write(node + " ");
}
Go Code
package main
import (
"container/list"
"fmt"
)
type BreadthFirstSearch struct{}
func (bfs *BreadthFirstSearch) buildGraph(edges [][]int, n int) [][]int {
graph := make([][]int, n)
for i := 0; i < n; i++ {
graph[i] = make([]int, 0)
}
for _, edge := range edges {
graph[edge[0]] = append(graph[edge[0]], edge[1])
graph[edge[1]] = append(graph[edge[1]], edge[0])
}
return graph
}
func (bfs *BreadthFirstSearch) breadthFirstSearch(edges [][]int, n, src int) []int {
graph := bfs.buildGraph(edges, n)
queue := list.New()
visited := make([]bool, n)
bfsAnswer := make([]int, n)
queue.PushBack(src)
visited[src] = true
index := 0
for queue.Len() > 0 {
currElement := queue.Front()
queue.Remove(currElement)
curr := currElement.Value.(int)
bfsAnswer[index] = curr
index++
for _, nbr := range graph[curr] {
if !visited[nbr] {
queue.PushBack(nbr)
visited[nbr] = true
}
}
}
return bfsAnswer
}
func main() {
edges := [][]int{{0, 1}, {0, 2}, {1, 2}, {1, 3}, {1, 4}, {2, 5}, {3, 4}, {3, 5}}
n := 6
src := 0
var breadthFirstSearch BreadthFirstSearch
bfsAnswer := breadthFirstSearch.breadthFirstSearch(edges, n, src)
for _, node := range bfsAnswer {
fmt.Printf("%d ", node)
}
}
Complexity Analysis
Time Complexity: O(V + E), where V is the number of nodes and E is the number of edges.
Space Complexity: O(V + E), where V is the number of nodes and E is the number of edges and this space is contributed by Adjacency List.
Follow us on LinkedIn and connect with us on Discord in case you are stuck or have any questions.