Greatest Common Divisor (Euclid's Algorithm)

Introduction

The Greatest Common Divisor (GCD) or the Highest Common Factor (HCF) of two numbers is the largest number that divides both of them. In other words, the Greatest Common Divisor (GCD) of two integers (a, b), denoted by gcd(a,b), is defined as the largest positive integer d such that d divides both a and b.

A straightforward approach to finding the GCD is to identify all prime factors of both numbers and then determine the intersection of all factors present in both numbers. Finally, the GCD is computed as the product of the elements in the intersection.

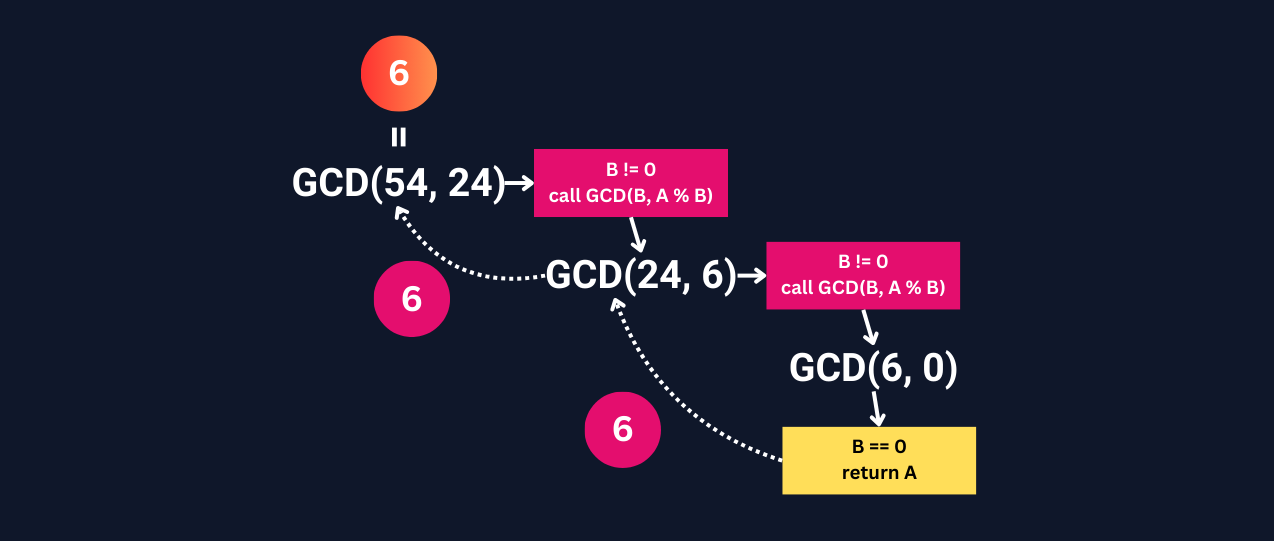
According to the Euclid’s Algorithm:

gcd(A, B) = gcd(B, A % B) // recurrence for GCD
gcd(A, 0) = A // base case

Proof

Let’s discuss the proof of the recurrence.

• Let us suppose, a = bq + r.
• Let d be any common divisor of a and b, which implies d divides a and d divides b implies that d divides (a – bq), which in turn implies that d divides r.
• Let e be any common divisor of b and r, which implies that e divides b and e divides r which implies that e divides (bq + r), which in turn implies that e divides a.
• Based on this observation, we can exploit the fact that the set of common divisors of a and b is the same as the set of common divisors of b and r. Therefore, we can recursively apply the GCD function to b and r, which are smaller numbers, instead of a and b. This leads to the recurrence relation:

gcd(a, b) = gcd(b, a % b)

The GCD of more than 2 numbers, e.g., gcd(a,b,c) is equal to gcd(a,gcd(b,c)) and so on.

Code

Java

public class GCD {
    public static int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

    public static void main(String[] args) {
        int a = 54, b = 24;
        int result = gcd(a, b);
        System.out.println(result);
    }
}

C++

#include <iostream>
using namespace std;

int gcd(int a, int b) {
    if(b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

int main() {
    int a = 54, b = 24;
    int result;
    result = gcd(a,b);
    cout << result;
}

Python

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

if __name__ == "__main__":
    a, b = 54, 24
    result = gcd(a, b)
    print(result)

Complexity Analysis

Time Complexity

• Euclid’s GCD algorithm runs in O(log(N)), where N = max(a,b).

Space Complexity

• Euclid’s GCD algorithm takes O(log(N)) space, where N = max(a,b). This is because all the recursive calls are stored in the stack.