Remove Interval
Problem Statement
A set of real numbers can be represented as the union of several disjoint intervals, where each interval is in the form [a, b). A real number x is in the set if one of its intervals [a, b) contains x (i.e. a <= x < b).
You are given a sorted list of disjoint intervals intervals representing a set of real numbers as described above, where intervals[i] = [ai, bi] represents the interval [ai, bi). You are also given another interval toBeRemoved.
Return the set of real numbers with the interval toBeRemoved removed from intervals. In other words, return the set of real numbers such that every x in the set is in intervals but not in toBeRemoved. Your answer should be a sorted list of disjoint intervals as described above.
Example 1
Input: intervals = [[0,2],[3,4],[5,7]], toBeRemoved = [1,6]
Output: [[0,1],[6,7]]
Explanation:
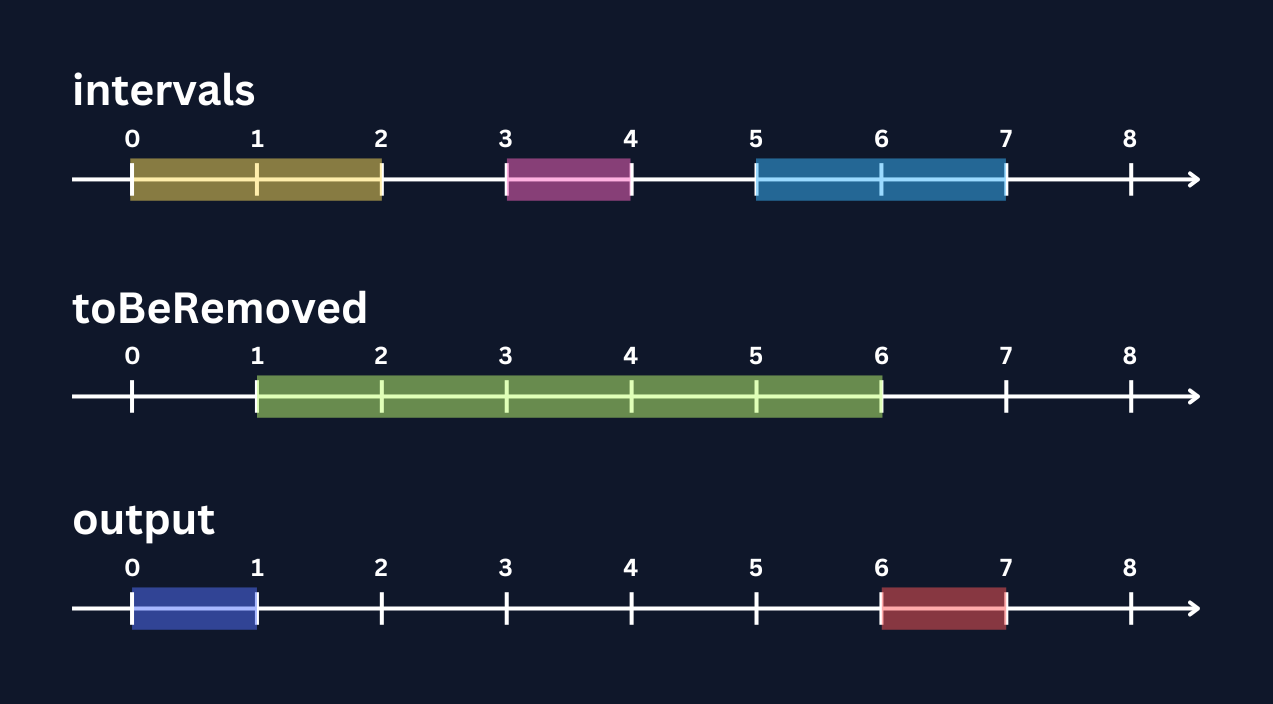
Example 2
Input: intervals = [[0,5]], toBeRemoved = [2,3]
Output: [[0,2],[3,5]]
Solution
The input is already sorted which means we need to do this at least in linear time complexity. Is it possible to do in O(log N)? No, because to copy input elements into output still requires O(N) time.
Let's visualise every single case to build our algorithm and intuition.
Case 1: When there is no overlap.
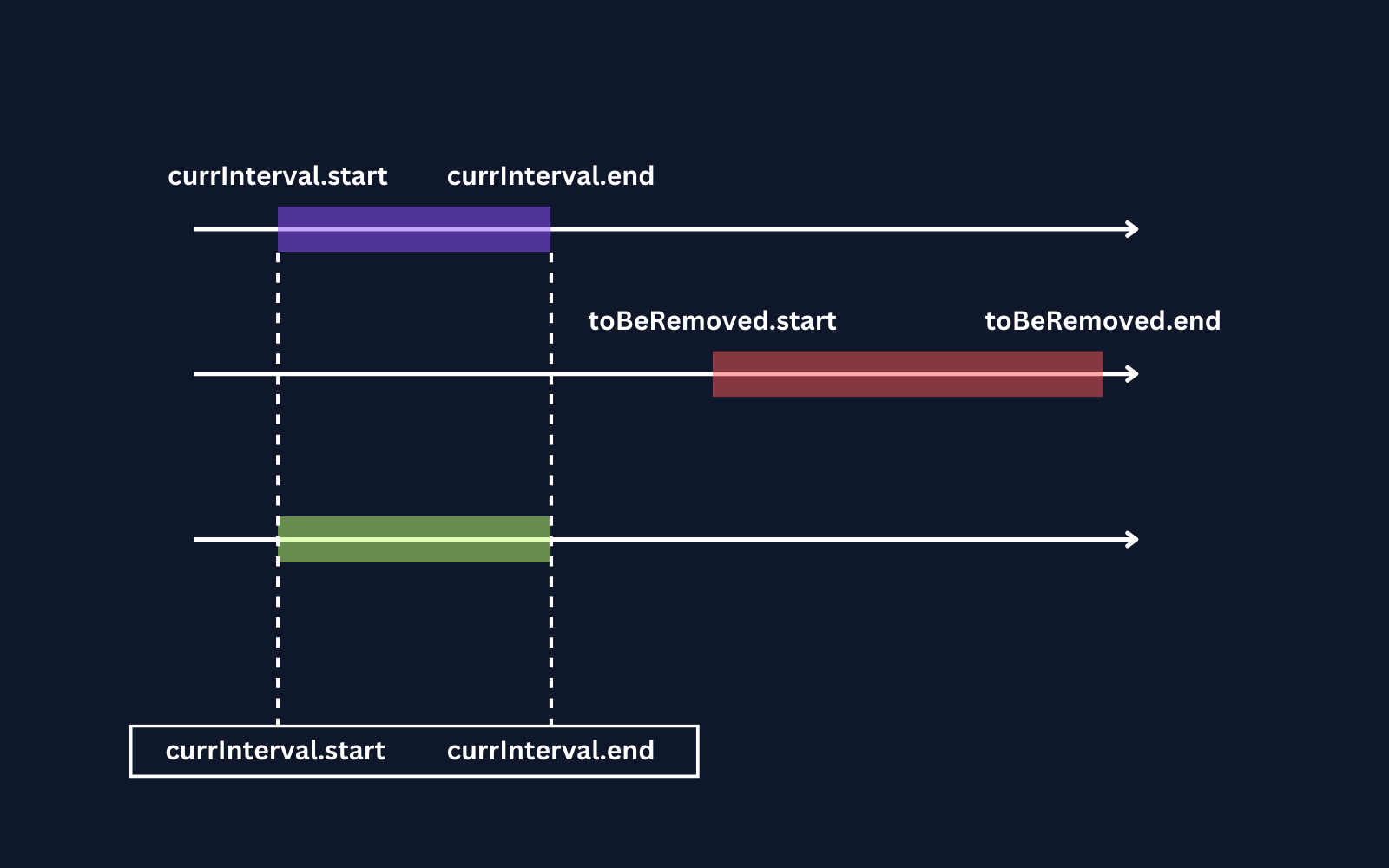
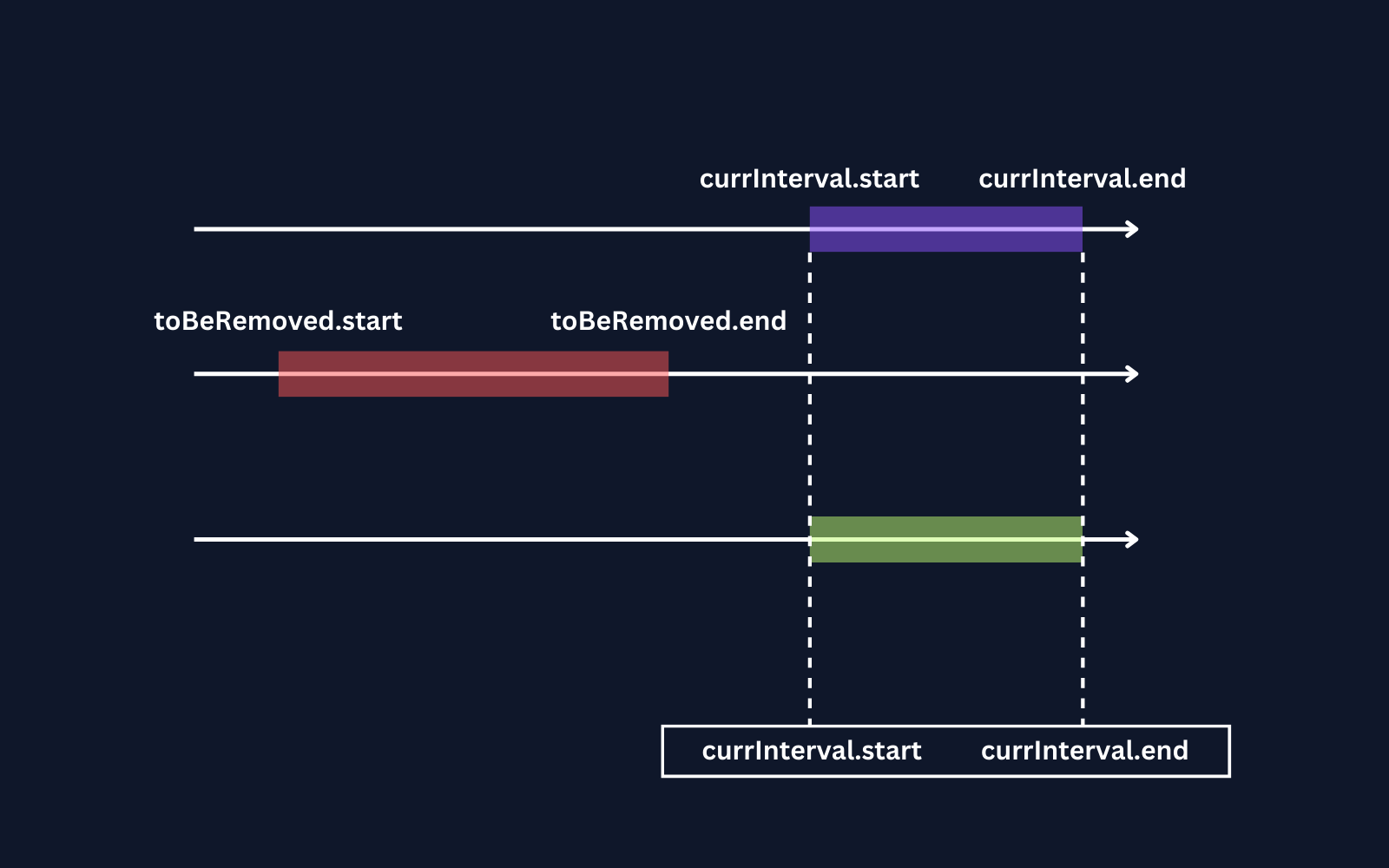
Both cases represents no overlapping of currInterval with toBeRemoved interval
Let's conclude this.
if(currInterval.end < toBeRemoved.start or currInterval.start > toBeRemoved.end) {
result.add([currInterval.start, currInterval.end]);
}
Case 2: When there is an overlapping and currInterval.start < toBeRemoved.start.
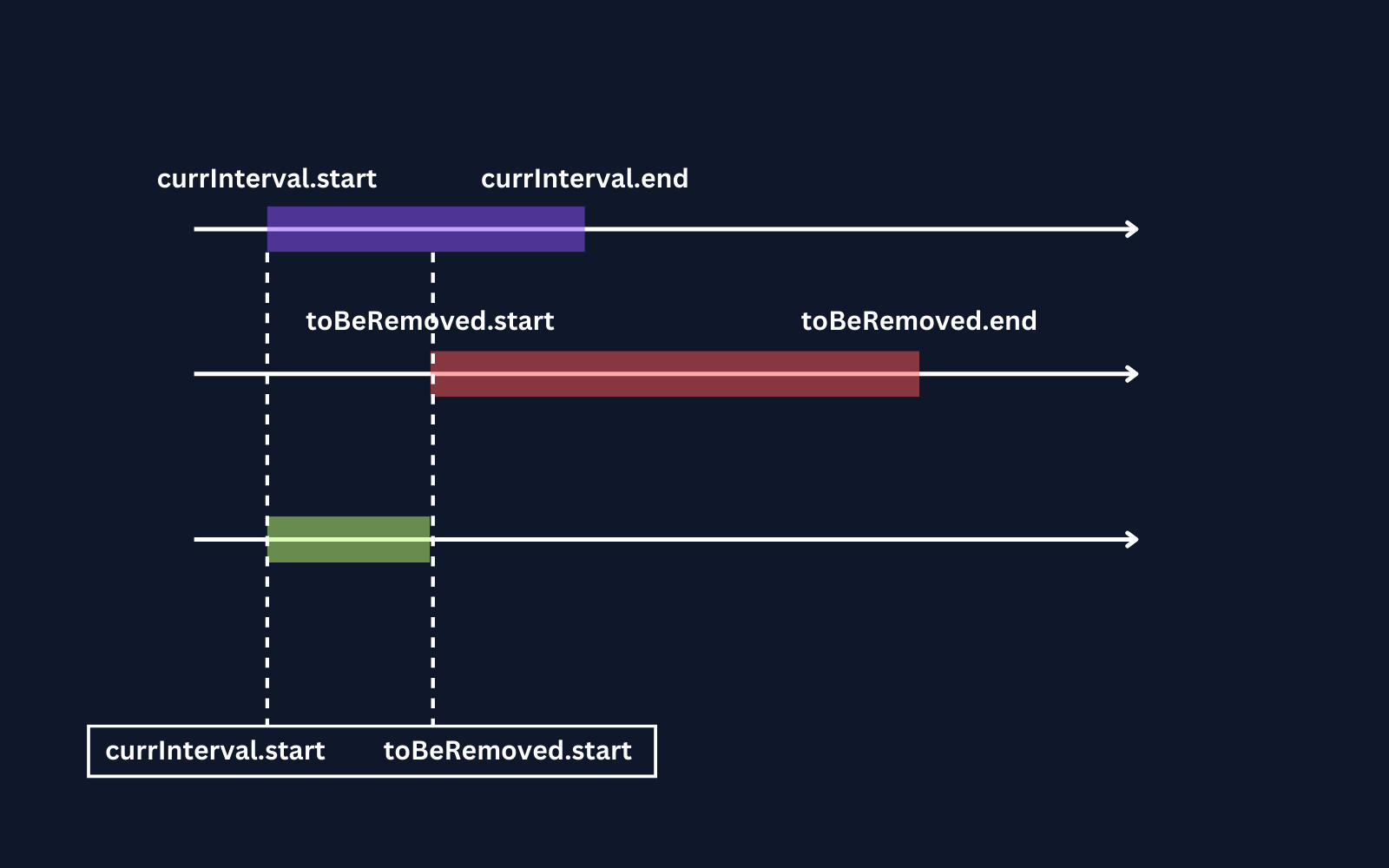
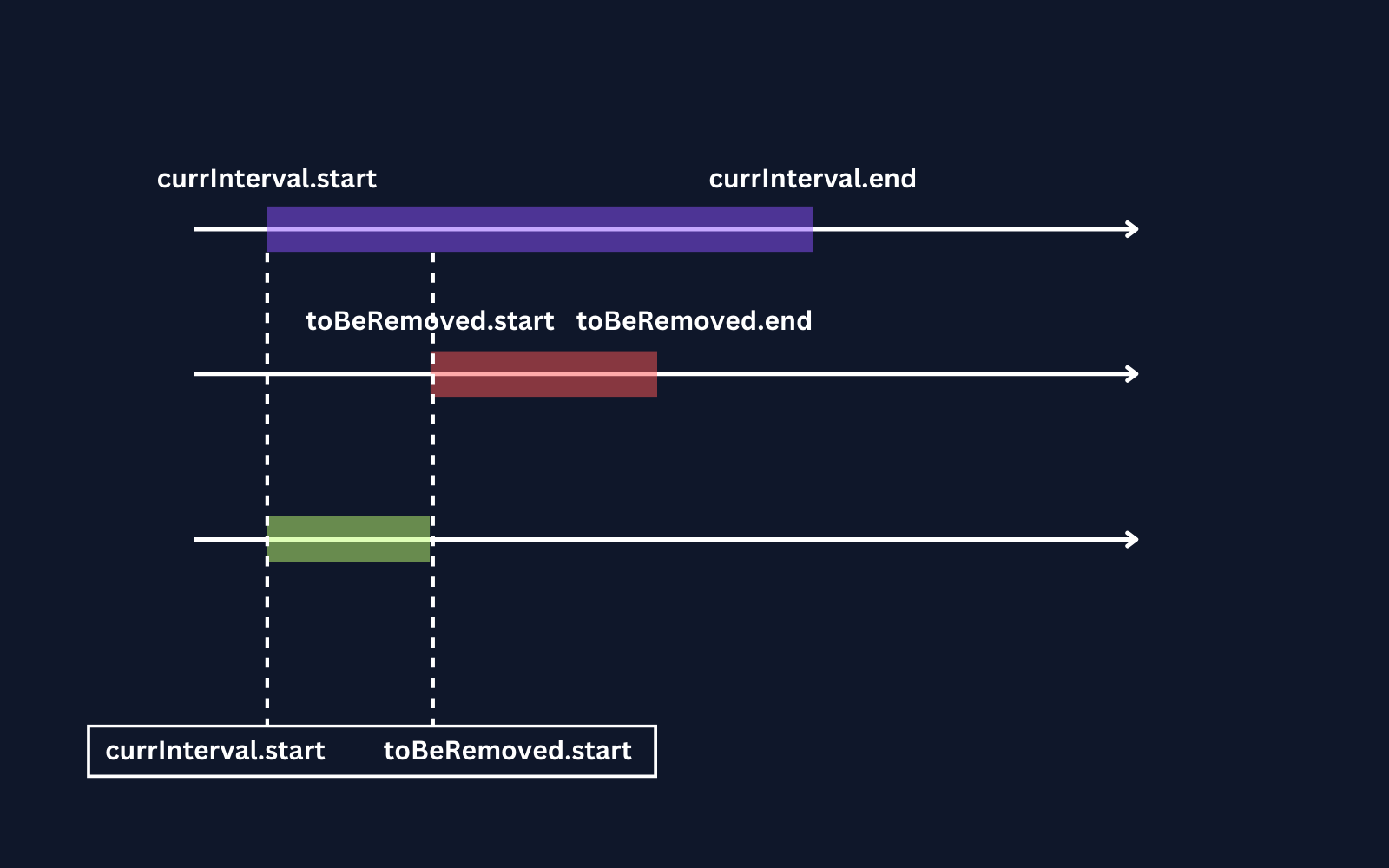
When there is overlap and currInterval.start < toBeRemoved.start
Let's conclude this.
if(currInterval.start < toBeRemoved.start) {
result.add([currInterval.start, toBeRemoved.start])
}
Case 3: When there is an overlapping and currInterval.end > toBeRemoved.end.
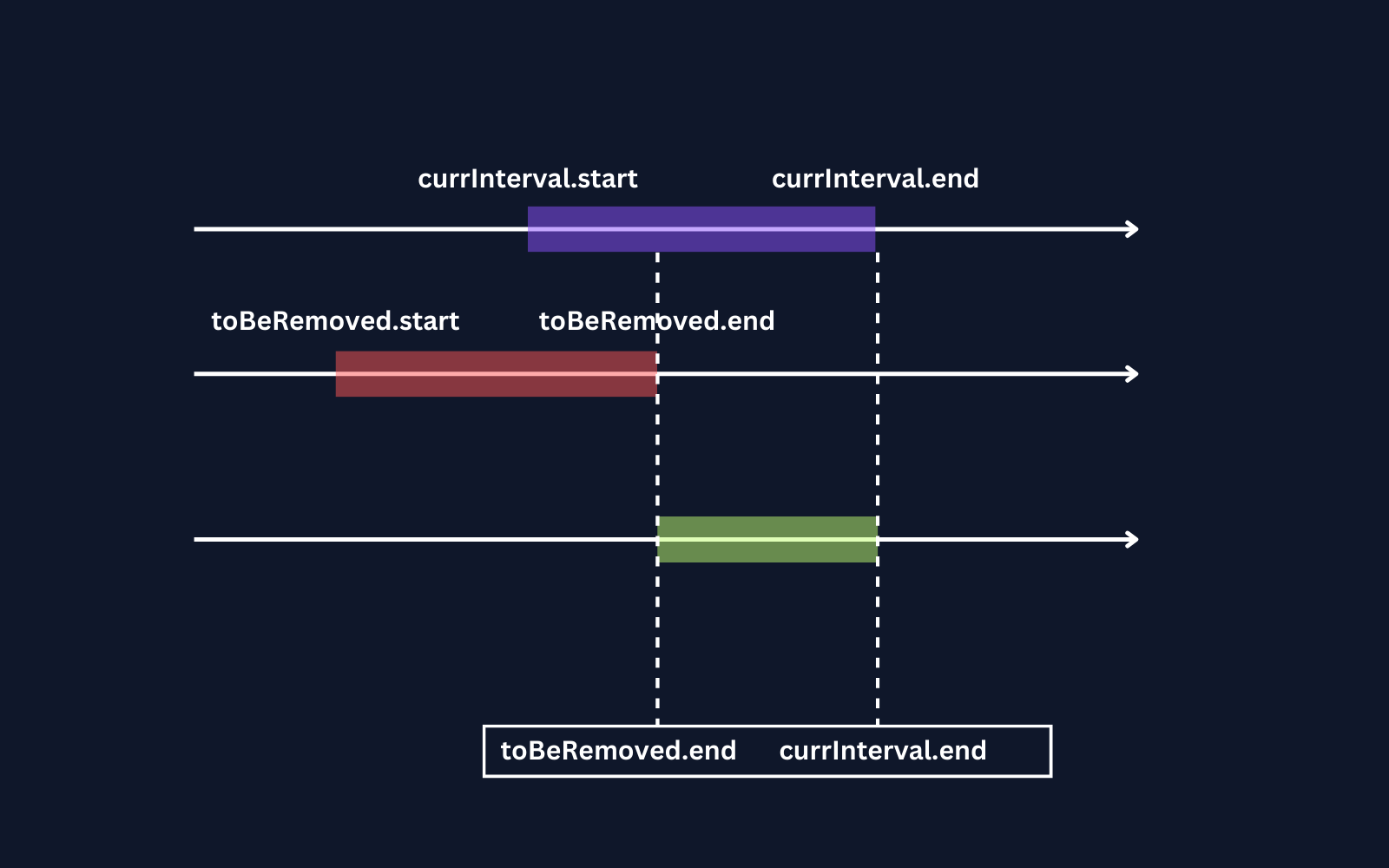
Let's conclude this.
if(currInterval.end > toBeRemoved.end) {
result.add([toBeRemoved.end, currInterval.end])
}
Case 4: Ignorable case, we will not consider this.
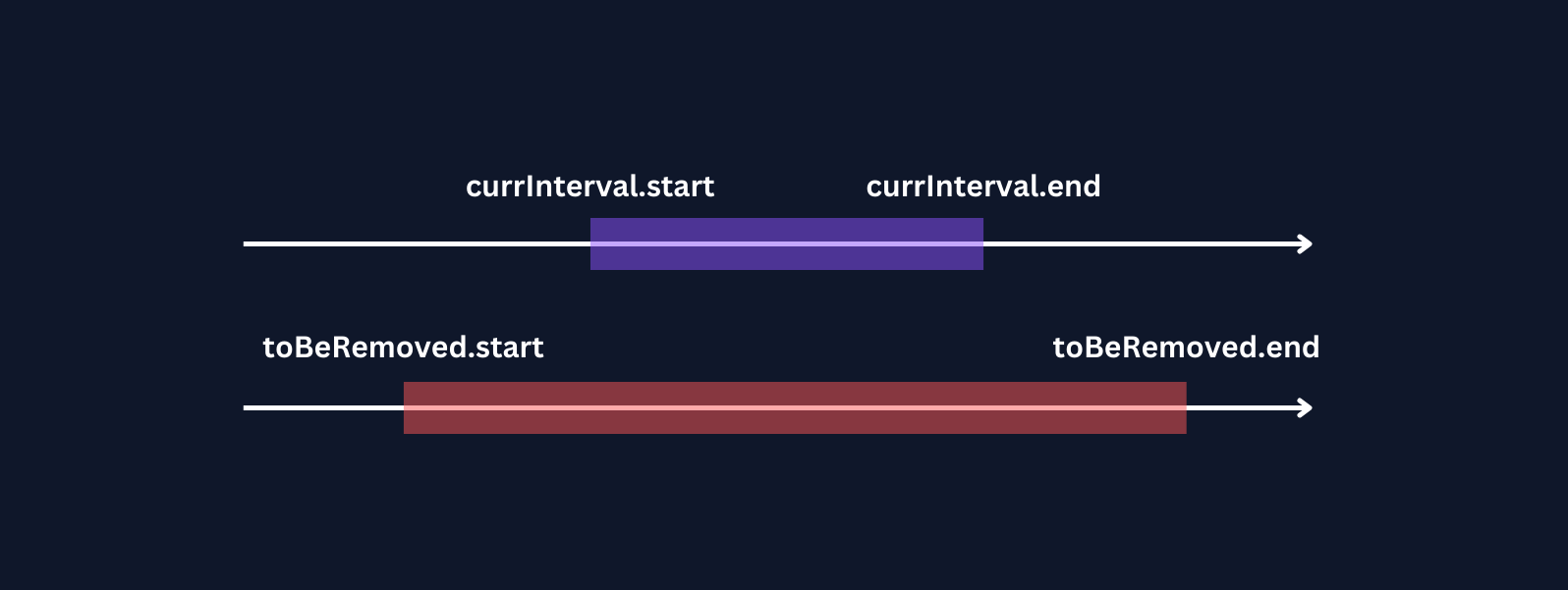
We will not have any condition for this case and hence this can be ignored.
Now, we just need to iterate over the list of intervals and apply these above set of conditions.
Java Code
import java.util.*;
class Innoskrit {
public static List<List<Integer>> removeInterval(int[][] intervals, int[] toBeRemoved) {
List<List<Integer>> result = new ArrayList<>();
for (int[] interval : intervals) {
if (interval[0] > toBeRemoved[1] || interval[1] < toBeRemoved[0]) {
result.add(Arrays.asList(interval[0], interval[1]));
} else {
if (interval[0] < toBeRemoved[0]) {
result.add(Arrays.asList(interval[0], toBeRemoved[0]));
}
if (interval[1] > toBeRemoved[1]) {
result.add(Arrays.asList(toBeRemoved[1], interval[1]));
}
}
}
return result;
}
public static void main(String[] args) {
int[][] intervals = new int[][]{{0, 2}, {3, 4}, {5, 7}};
int[] toBeRemoved = new int[]{1, 6};
List<List<Integer>> result = Innoskrit.removeInterval(intervals, toBeRemoved);
for (List<Integer> interval : result)
System.out.print("[" + interval.get(0) + "," + interval.get(1) + "] ");
System.out.println();
}
}
C++ Code
#include <bits/stdc++.h>
using namespace std;
class Innoskrit {
public:
static vector<vector<int>> removeInterval(vector<vector<int>>& intervals, vector<int>& toBeRemoved) {
vector<vector<int>> result;
for (const auto& interval : intervals) {
if (interval[0] > toBeRemoved[1] || interval[1] < toBeRemoved[0]) {
result.push_back({interval[0], interval[1]});
} else {
if (interval[0] < toBeRemoved[0]) {
result.push_back({interval[0], toBeRemoved[0]});
}
if (interval[1] > toBeRemoved[1]) {
result.push_back({toBeRemoved[1], interval[1]});
}
}
}
return result;
}
};
int main() {
vector<vector<int>> intervals = {{0, 2}, {3, 4}, {5, 7}};
vector<int> toBeRemoved = {1, 6};
vector<vector<int>> result = Innoskrit::removeInterval(intervals, toBeRemoved);
for (const auto& interval : result)
cout << "[" << interval[0] << "," << interval[1] << "] ";
cout << endl;
return 0;
}
Python Code
class Innoskrit:
def removeInterval(self, intervals, toBeRemoved):
result = []
for interval in intervals:
if interval[0] > toBeRemoved[1] or interval[1] < toBeRemoved[0]:
result.append([interval[0], interval[1]])
else:
if interval[0] < toBeRemoved[0]:
result.append([interval[0], toBeRemoved[0]])
if interval[1] > toBeRemoved[1]:
result.append([toBeRemoved[1], interval[1]])
return result
if __name__ == "__main__":
intervals = [[0, 2], [3, 4], [5, 7]]
toBeRemoved = [1, 6]
result = Innoskrit().removeInterval(intervals, toBeRemoved)
for interval in result:
print(f"[{interval[0]},{interval[1]}]", end=" ")
print()
Output
[0,1] [6, 7]
Time Complexity
O(N) since it's one pass along the input array.
Space Complexity
O(1) without considering O(N) space for the output list.