Sum of Left Leaves - LeetCode Daily Challenge

Problem Statement

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1

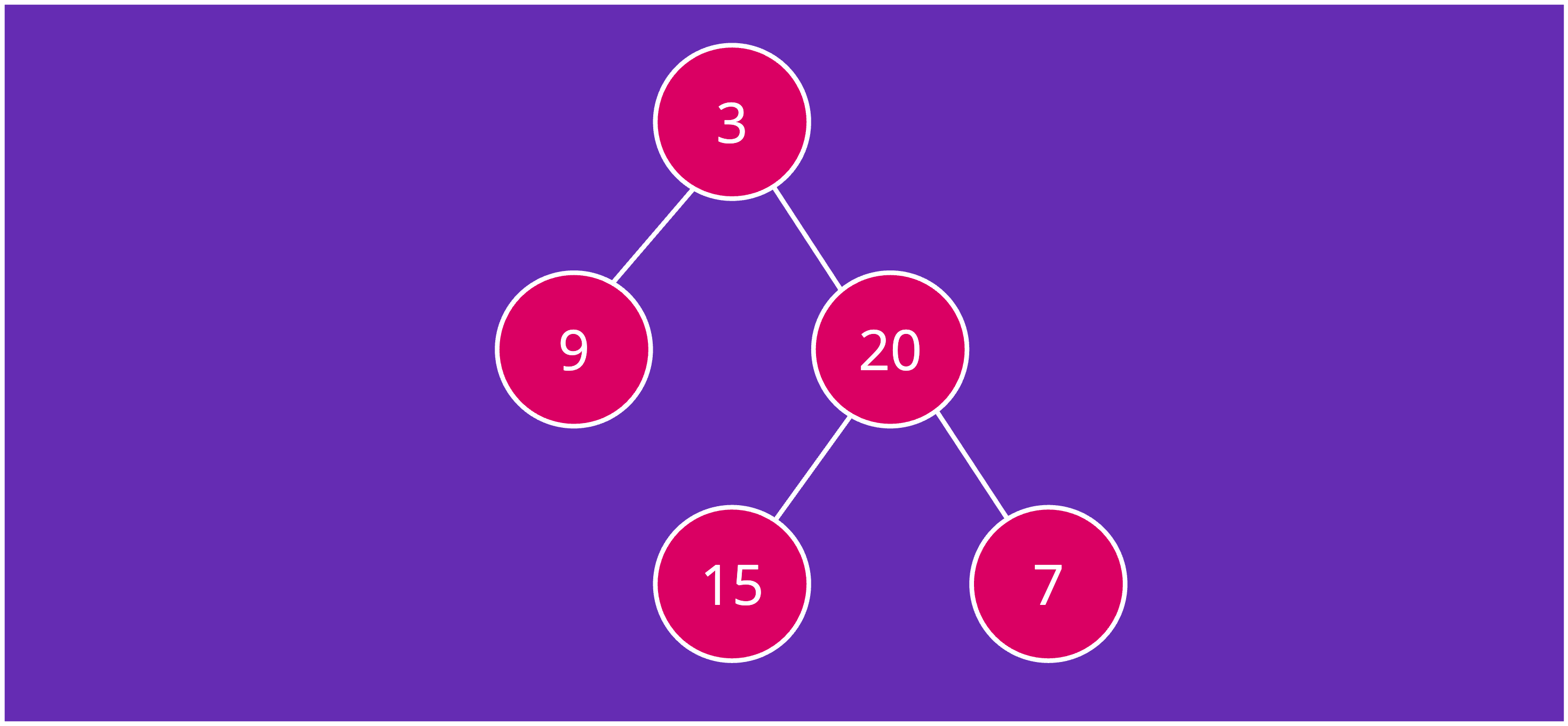
Input: root = [3,9,20,null,null,15,7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2

Input: root = [1]
Output: 0

Try here before watching the video.

Video Solution

Java Code

class Solution {
    int sum = 0;
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null) return 0;
        if(root.left != null) {
            if(root.left.left == null && root.left.right == null) {
                sum += root.left.val;
            }
        }

        sumOfLeftLeaves(root.left);
        sumOfLeftLeaves(root.right);

        return sum;
    }
}

C++ Code

class Solution {
public:
    int sum = 0;
    int sumOfLeftLeaves(TreeNode* root) {
        if(root == NULL) return 0;
        if(root->left != NULL) {
            if(root->left->left == NULL && root->left->right == NULL) {
                sum += root->left->val;
            }
        }
        sumOfLeftLeaves(root->left);
        sumOfLeftLeaves(root->right);
        return sum;
    }
};

Python Code

class Solution(object):
    def __init__(self):
        self.sum = 0
    
    def sumOfLeftLeaves(self, root):
        if not root:
            return 0
        if root.left and not root.left.left and not root.left.right:
            self.sum += root.left.val
        self.sumOfLeftLeaves(root.left)
        self.sumOfLeftLeaves(root.right)
        return self.sum

Javascript Code

var sumOfLeftLeaves = function(root) {
    let sum = 0;
    const traverse = (node) => {
        if (!node) return;
        if (node.left && !node.left.left && !node.left.right) {
            sum += node.left.val;
        }
        traverse(node.left);
        traverse(node.right);
    }
    traverse(root);
    return sum;
};

Go Code

func sumOfLeftLeaves(root *TreeNode) int {
    var sum int
    var traverse func(node *TreeNode)
    traverse = func(node *TreeNode) {
        if node == nil {
            return
        }
        if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
            sum += node.Left.Val
        }
        traverse(node.Left)
        traverse(node.Right)
    }
    traverse(root)
    return sum
}

Complexity Analysis

Time Complexity: O(N), we shall iterate over all the nodes.
Space Complexity: O(N), the tree might be skewed in the worst case and therefore the stack might occupy N space for storing recursive calls.