Diameter of Binary Tree - LeetCode Daily Challenge

Problem Statement

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1

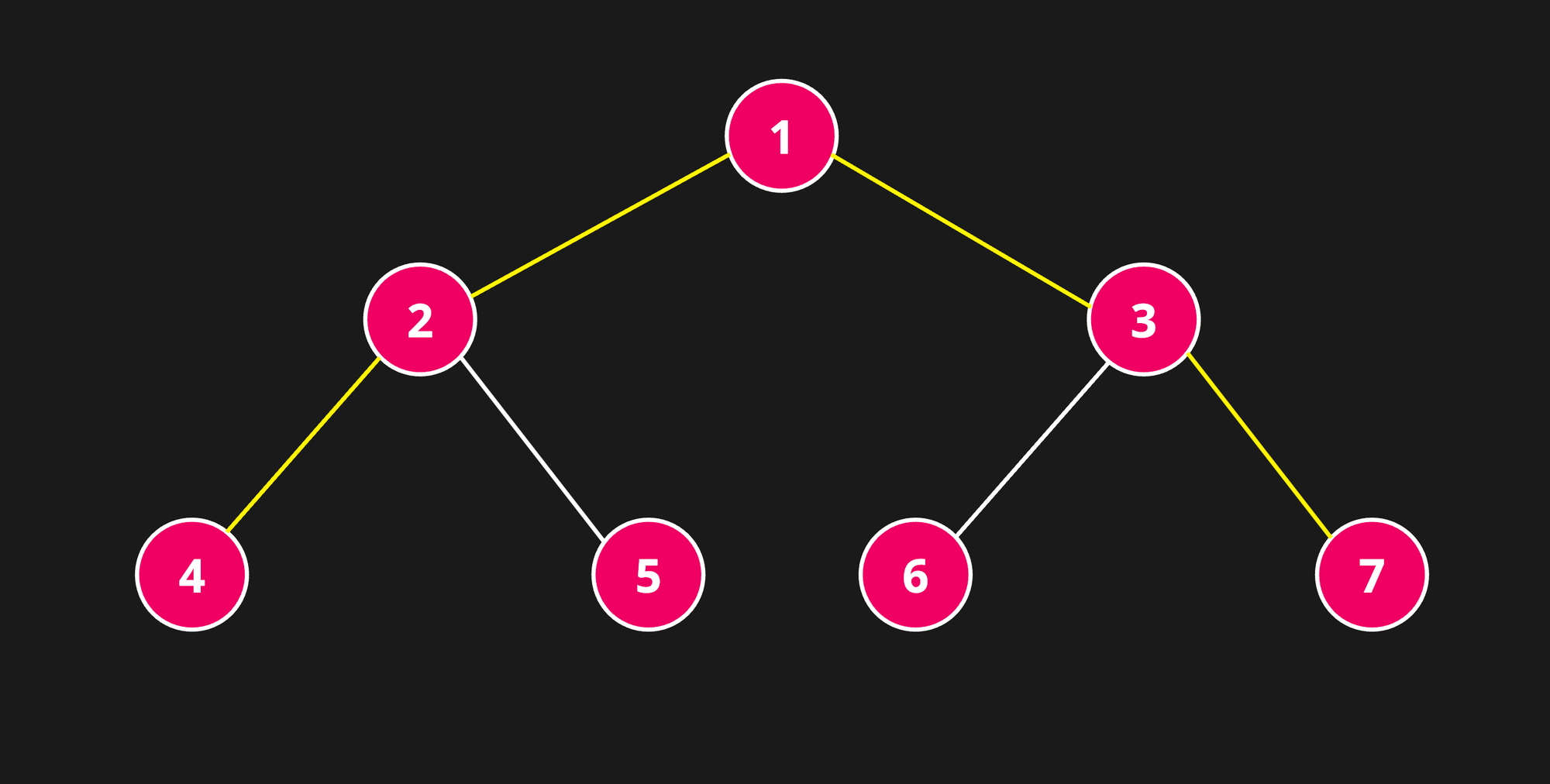
Input: root = [1,2,3,4,5,6,7]
Output: 4
Explanation: 4 is the length of the path [4,2,1,3,6], [4,2,1,3,7], [5,2,1,3,6] or [5,2,1,3,7].

Example 2

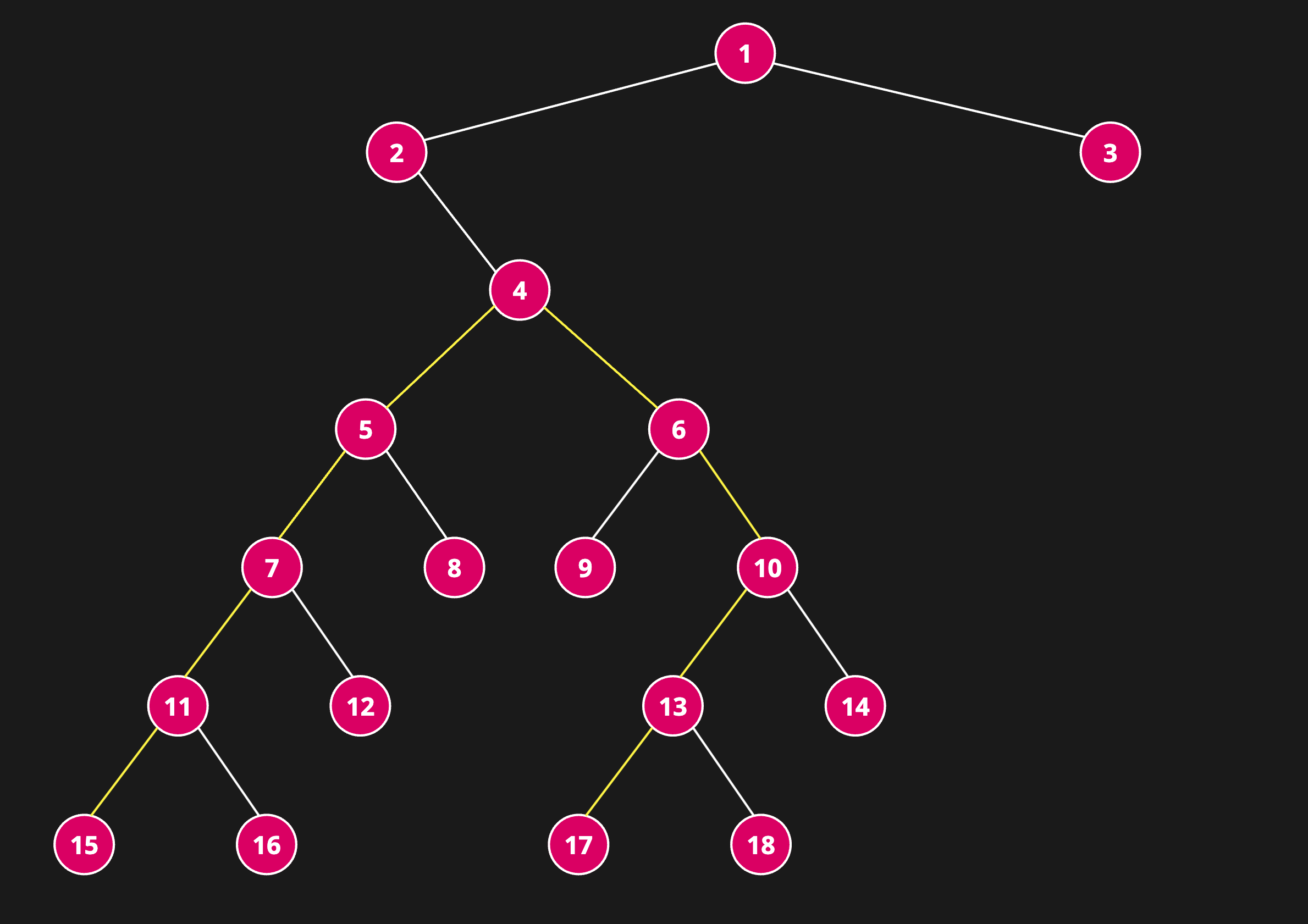
Input: root = [1,2,3,null,4,null,null,5,6,7,8,9,10,11,12,null,null,null,null,13,14,15,16,null,null,17,18]
Output: 8
Explanation: 8 is the length of the path [15,11,7,5,4,6,10,13,17], [15,11,7,5,4,6,10,13,18], [16,11,7,5,4,6,10,13,17] or [16,11,7,5,4,6,10,13,18].

Try here before watching the video.

Video Solution

Java Code

class Solution {
    int diameter = 0;
    private int height(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        int currDiameter = 1 + leftHeight + rightHeight;
        diameter = Math.max(currDiameter, diameter);
        return 1 + Math.max(leftHeight, rightHeight);
    }
    public int diameterOfBinaryTree(TreeNode root) {
        height(root);
        return diameter - 1;
    }
}

C++ Code

class Solution {
public:
    int diameter = 0;
    int height(TreeNode* root) {
        if(root == NULL) {
            return 0;
        }
        int leftHeight = height(root->left);
        int rightHeight = height(root->right);
        int currDiameter = 1 + leftHeight + rightHeight;
        diameter = max(currDiameter, diameter);
        return 1 + max(leftHeight, rightHeight);
    }
    int diameterOfBinaryTree(TreeNode* root) {
        height(root);
        return diameter - 1;
    }
};

Python Code

class Solution:

    # diameter variable is bound to every new test case.
    # hence, associate it with self so that it is different for every new test case.
    # to understand this, oops principles must be known to you.
    def __init__(self):  
        self.diameter = 0

    def height(self, root):
        if root is None:
            return 0
        leftHeight = self.height(root.left)
        rightHeight = self.height(root.right)
        currDiameter = 1 + leftHeight + rightHeight
        self.diameter = max(currDiameter, self.diameter)
        return 1 + max(leftHeight, rightHeight)
    
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        self.height(root)
        return self.diameter - 1

Javascript Code

var diameterOfBinaryTree = function(root) {
    let diameter = 0;

    const height = function(node) {
        if (node === null) {
            return 0;
        }

        let leftHeight = height(node.left);
        let rightHeight = height(node.right);
        let currDiameter = 1 + leftHeight + rightHeight;
        diameter = Math.max(currDiameter, diameter);

        return 1 + Math.max(leftHeight, rightHeight);
    };

    height(root);
    return diameter - 1;
};

Go Code

type Solution struct {
	diameter int
}

func (sol *Solution) height(root *TreeNode) int {
	if root == nil {
		return 0
	}

	leftHeight := sol.height(root.Left)
	rightHeight := sol.height(root.Right)
	currDiameter := 1 + leftHeight + rightHeight
	sol.diameter = int(math.Max(float64(currDiameter), float64(sol.diameter)))

	return 1 + int(math.Max(float64(leftHeight), float64(rightHeight)))
}

func diameterOfBinaryTree(root *TreeNode) int {
    sol := Solution{diameter: 0}
	sol.height(root)
	return sol.diameter - 1
}

Complexity Analysis

Time Complexity: O(N), we are iterating over N number of nodes in the tree.
Space Complexity: O(N), in the worst-case scenario, the tree can be skewed. Therefore, the total number of active recursive calls in the stack can be N.