Problem Statement
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1
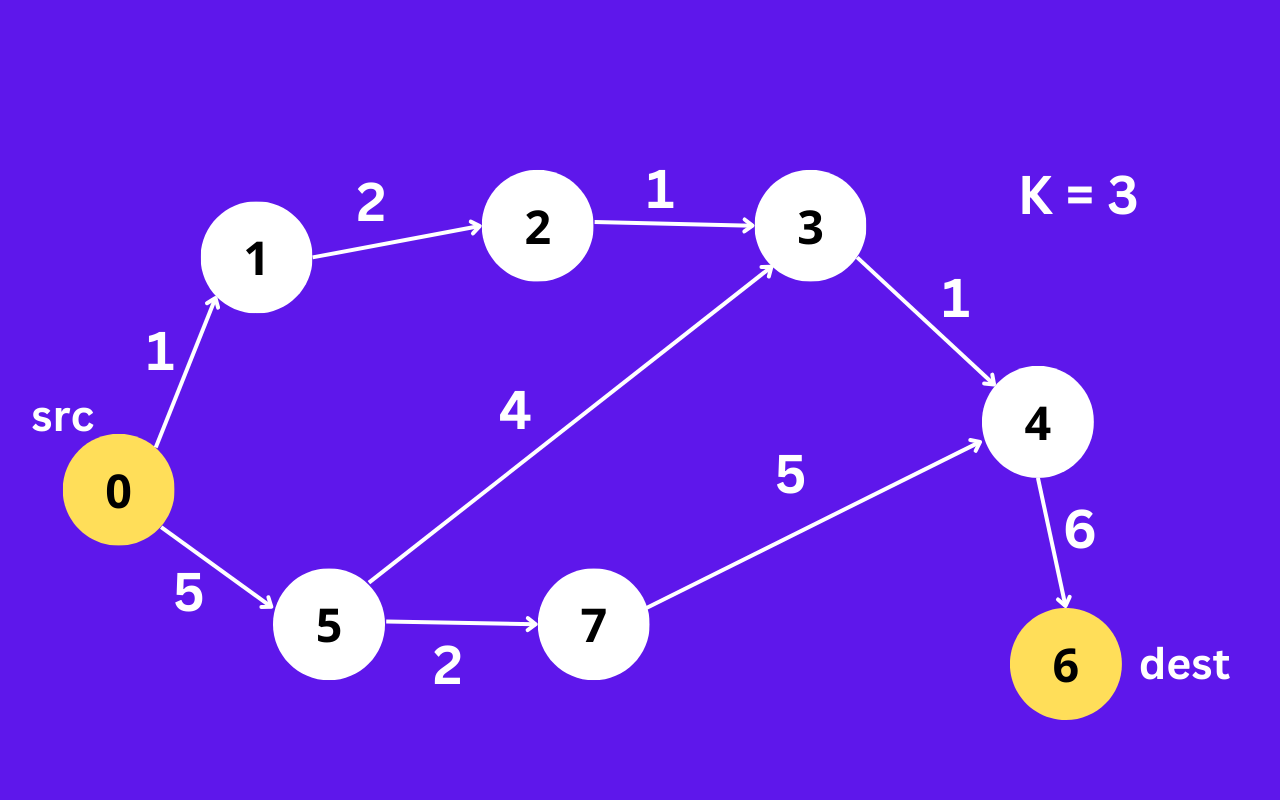
Input: n = 8, flights = [[0,1,1],[0,5,5],[1,2,2],[2,3,1],[3,4,1],[4,6,6],[5,3,4],[5,7,2],[7,4,5]], src = 0, dst = 6, k = 3
Output: 16
Explanation:
The graph is shown above.
The optimal path with at most 3 stop from city 0 to 3 is 0 -> 5 -> 3 -> 4 -> 6 with minimum cost of 16.
Note that the path through cities [0,1,2,3,4,6] is cheaper but is invalid because it uses 4 stops.Example 2
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Try here before watching the video.
Video Explanation
Java Code
class Pair {
int node, distance;
public Pair(int node, int distance) {
this.node = node;
this.distance = distance;
}
}
class Node {
int node, distance, stops;
public Node(int node, int distance, int stops) {
this.node = node;
this.distance = distance;
this.stops = stops;
}
}
class Solution {
private List<List<Pair>> buildGraph(int[][] flights, int n) {
List<List<Pair>> graph = new ArrayList<>();
for(int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
for(int[] flight : flights) {
graph.get(flight[0]).add(new Pair(flight[1], flight[2]));
}
return graph;
}
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
List<List<Pair>> graph = buildGraph(flights, n);
int[] distance = new int[n];
int[] stops = new int[n];
Arrays.fill(distance, Integer.MAX_VALUE);
Arrays.fill(stops, Integer.MAX_VALUE);
PriorityQueue<Node> minHeap = new PriorityQueue<>((node1, node2) -> node1.distance - node2.distance);
distance[src] = 0;
stops[src] = 0;
minHeap.add(new Node(src, distance[src], stops[src]));
while(!minHeap.isEmpty()) {
Node curr = minHeap.poll();
int currNode = curr.node;
int currDistance = curr.distance;
int currStops = curr.stops;
if(currNode == dst) return currDistance;
if(currStops == k + 1) continue;
for(Pair pair : graph.get(currNode)) {
int nbrNode = pair.node;
int nbrDistance = pair.distance;
if((currDistance + nbrDistance) < distance[nbrNode]) {
distance[nbrNode] = currDistance + nbrDistance;
stops[nbrNode] = currStops + 1;
minHeap.add(new Node(nbrNode, distance[nbrNode], stops[nbrNode]));
} else if((currStops + 1) < stops[nbrNode]) {
minHeap.add(new Node(nbrNode, currDistance + nbrDistance, currStops + 1));
}
}
}
return -1;
}
}
C++ Code
class Node {
public:
int node, distance, stops;
Node(int node, int distance, int stops) {
this->node = node;
this->distance = distance;
this->stops = stops;
}
};
class Solution {
public:
struct comparator {
bool operator() (Node a, Node b) {
return a.distance > b.distance;
}
};
vector<vector<pair<int, int>>> buildGraph(int n, vector<vector<int>>& flights) {
vector<vector<pair<int, int>>> graph;
for(int i = 0; i < n; i++) {
vector<pair<int, int>> v;
graph.push_back(v);
}
for(auto flight : flights) {
graph[flight[0]].push_back(make_pair(flight[1], flight[2]));
}
return graph;
}
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
vector<vector<pair<int, int>>> graph = buildGraph(n, flights);
priority_queue<Node, vector<Node>, comparator> minHeap;
vector<int> distance(n, INT_MAX);
vector<int> stops(n, INT_MAX);
distance[src] = 0;
stops[src] = 0;
minHeap.push(Node(src, 0, 0));
while(!minHeap.empty()) {
Node curr = minHeap.top();
minHeap.pop();
int currNode = curr.node;
int currDistance = curr.distance;
int currStops = curr.stops;
if(currNode == dst) return currDistance;
if(currStops == k + 1) continue;
for(auto pair : graph[currNode]) {
int nbrNode = pair.first;
int nbrDistance = pair.second;
if(currDistance + nbrDistance < distance[nbrNode]) {
distance[nbrNode] = currDistance + nbrDistance;
stops[nbrNode] = currStops + 1;
minHeap.push(Node(nbrNode, distance[nbrNode], stops[nbrNode]));
} else if(currStops + 1 < stops[nbrNode]) {
minHeap.push(Node(nbrNode, currDistance + nbrDistance, currStops + 1));
}
}
}
return -1;
}
};
Python Code
class Solution:
def build_graph(n, flights):
graph = []
for i in range(n):
graph.append(list()) # graph = [[], [], [], [], []]
for flight in flights:
graph[flight[0]].append((flight[1], flight[2]))
return graph
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
graph = Solution.build_graph(n, flights)
min_heap = []
distance = [math.inf] * n
stops = [math.inf] * n
distance[src] = 0
stops[src] = 0
heappush(min_heap, (0, 0, src))
while min_heap:
curr_dist, curr_stop, curr_node = heappop(min_heap)
if curr_node == dst:
return curr_dist
if curr_stop == k + 1:
continue
for nbr, dist in graph[curr_node]:
if curr_dist + dist < distance[nbr]:
distance[nbr] = curr_dist + dist
stops[nbr] = curr_stop + 1
heappush(min_heap, (distance[nbr], stops[nbr], nbr))
elif curr_stop + 1 < stops[nbr]:
heappush(min_heap, (curr_dist + dist, curr_stop + 1, nbr))
return -1
Go Code
type Pair struct {
node int
distance int
}
type Node struct {
node int
distance int
stops int
}
type MinHeap []Node
func (h MinHeap) Len() int { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].distance < h[j].distance }
func (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) {
*h = append(*h, x.(Node))
}
func (h *MinHeap) Pop() interface{} {
old := *h
n := len(old)
item := old[n-1]
*h = old[0 : n-1]
return item
}
func buildGraph(n int, flights [][]int) [][]Pair {
graph := make([][]Pair, n)
for _, flight := range flights {
start, end, distance := flight[0], flight[1], flight[2]
graph[start] = append(graph[start], Pair{end, distance})
}
return graph
}
func findCheapestPrice(n int, flights [][]int, src int, dst int, k int) int {
graph := buildGraph(n, flights)
distance := make([]int, n)
stops := make([]int, n)
for i := range distance {
distance[i] = int(1e9)
stops[i] = int(1e9)
}
minHeap := &MinHeap{}
heap.Init(minHeap)
distance[src] = 0
stops[src] = 0
heap.Push(minHeap, Node{src, distance[src], stops[src]})
for minHeap.Len() > 0 {
curr := heap.Pop(minHeap).(Node)
currNode := curr.node
currDistance := curr.distance
currStops := curr.stops
if currNode == dst {
return currDistance
}
if currStops == k+1 {
continue
}
for _, pair := range graph[currNode] {
nbrNode := pair.node
nbrDistance := pair.distance
newDistance := currDistance + nbrDistance
newStops := currStops + 1
if newDistance < distance[nbrNode] {
distance[nbrNode] = newDistance
stops[nbrNode] = newStops
heap.Push(minHeap, Node{nbrNode, newDistance, newStops})
} else if newStops < stops[nbrNode] {
heap.Push(minHeap, Node{nbrNode, newDistance, newStops})
}
}
}
return -1
}
Complexity Analysis
Time Complexity: O(V log V)
Space Complexity: O(E + V), where E is the number of edges and V is the number of vertices.
