Problem Statement
Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.
Note that the root node is at depth 1.
The adding rule is:
- Given the integer
depth, for each not null tree nodecurat the depthdepth - 1, create two tree nodes with valuevalascur's left subtree root and right subtree root. cur's original left subtree should be the left subtree of the new left subtree root.cur's original right subtree should be the right subtree of the new right subtree root.- If
depth == 1that means there is no depthdepth - 1at all, then create a tree node with valuevalas the new root of the whole original tree, and the original tree is the new root's left subtree.
Example 1
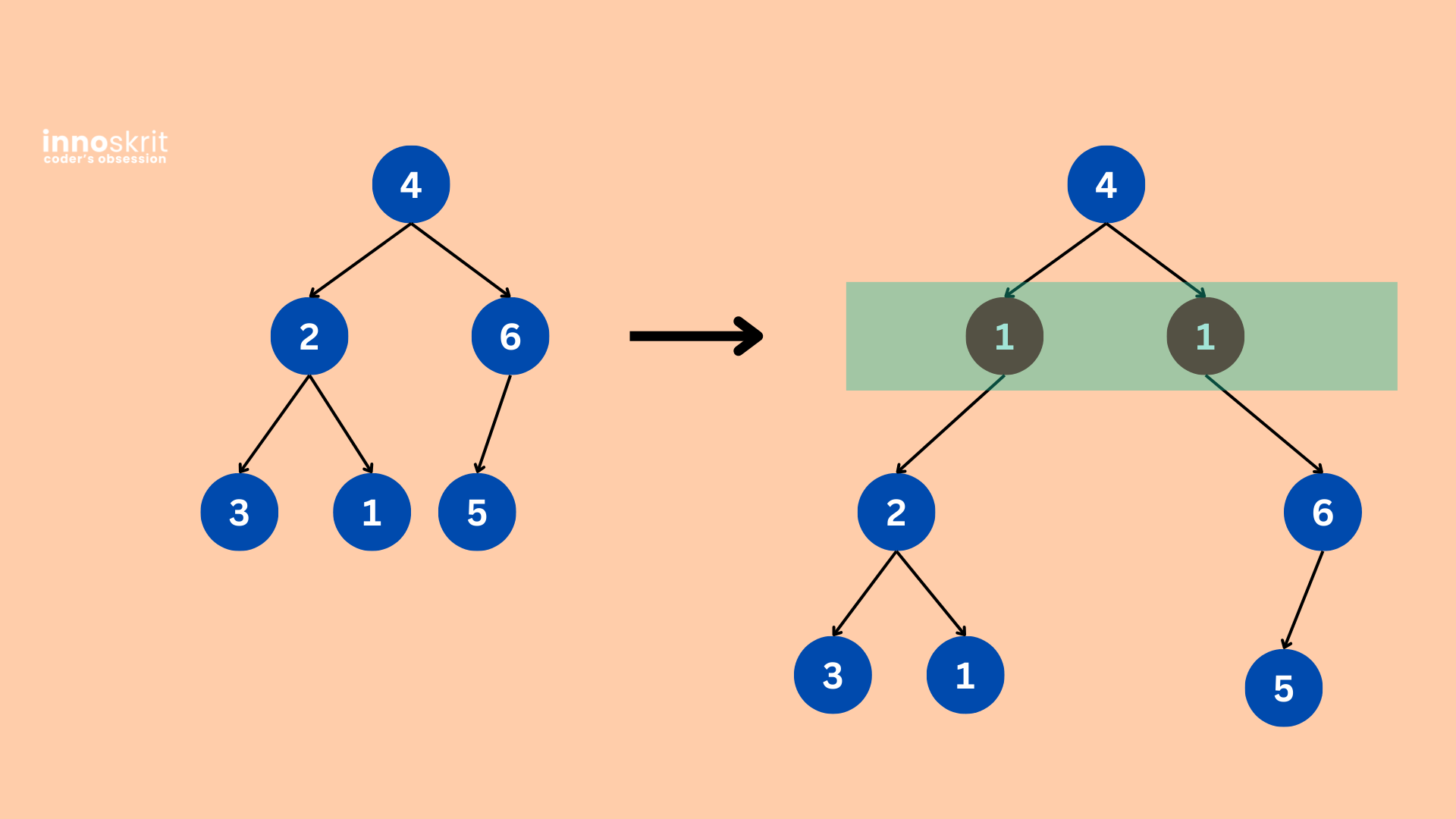
Input: root = [4,2,6,3,1,5], val = 1, depth = 2
Output: [4,1,1,2,null,null,6,3,1,5]
Example 2
Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]
Try here before watching the video.
Video Solution
Java Code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode addOneRow(TreeNode root, int val, int depth) {
if(depth == 1) {
TreeNode newRoot = new TreeNode(val);
newRoot.left = root;
return newRoot;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(--depth > 1) {
int size = queue.size();
for(int i = 0; i < size; i++) {
TreeNode curr = queue.poll();
if(curr.left != null) {
queue.add(curr.left);
}
if(curr.right != null) {
queue.add(curr.right);
}
}
}
while(!queue.isEmpty()) {
TreeNode curr = queue.poll();
TreeNode left = curr.left, right = curr.right;
TreeNode newLeft = new TreeNode(val), newRight = new TreeNode(val);
curr.left = newLeft;
curr.right = newRight;
newLeft.left = left;
newRight.right = right;
}
return root;
}
}
C++ Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
if (depth == 1) {
TreeNode* newRoot = new TreeNode(val);
newRoot->left = root;
return newRoot;
}
queue<TreeNode*> queue;
queue.push(root);
while (--depth > 1) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode* curr = queue.front();
queue.pop();
if (curr->left != nullptr) {
queue.push(curr->left);
}
if (curr->right != nullptr) {
queue.push(curr->right);
}
}
}
while (!queue.empty()) {
TreeNode* curr = queue.front();
queue.pop();
TreeNode* left = curr->left, *right = curr->right;
TreeNode* newLeft = new TreeNode(val), *newRight = new TreeNode(val);
curr->left = newLeft;
curr->right = newRight;
newLeft->left = left;
newRight->right = right;
}
return root;
}
};
Python Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:
if depth == 1:
new_root = TreeNode(val)
new_root.left = root
return new_root
queue = [root]
depth -= 1
while depth > 1:
size = len(queue)
for _ in range(size):
curr = queue.pop(0)
if curr.left:
queue.append(curr.left)
if curr.right:
queue.append(curr.right)
depth -= 1
while queue:
curr = queue.pop(0)
left, right = curr.left, curr.right
new_left, new_right = TreeNode(val), TreeNode(val)
curr.left = new_left
curr.right = new_right
new_left.left = left
new_right.right = right
return root
Javascript Code
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} val
* @param {number} depth
* @return {TreeNode}
*/
var addOneRow = function(root, val, depth) {
if (depth === 1) {
const newRoot = new TreeNode(val);
newRoot.left = root;
return newRoot;
}
const queue = [root];
while (--depth > 1) {
const size = queue.length;
for (let i = 0; i < size; i++) {
const curr = queue.shift();
if (curr.left) {
queue.push(curr.left);
}
if (curr.right) {
queue.push(curr.right);
}
}
}
while (queue.length) {
const curr = queue.shift();
const left = curr.left, right = curr.right;
const newLeft = new TreeNode(val), newRight = new TreeNode(val);
curr.left = newLeft;
curr.right = newRight;
newLeft.left = left;
newRight.right = right;
}
return root;
};
Go Code
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func addOneRow(root *TreeNode, val int, depth int) *TreeNode {
if depth == 1 {
newRoot := &TreeNode{Val: val}
newRoot.Left = root
return newRoot
}
queue := []*TreeNode{root}
depth -= 1
for depth > 1 {
size := len(queue)
for i := 0; i < size; i++ {
curr := queue[0]
queue = queue[1:]
if curr.Left != nil {
queue = append(queue, curr.Left)
}
if curr.Right != nil {
queue = append(queue, curr.Right)
}
}
depth--
}
for len(queue) > 0 {
curr := queue[0]
queue = queue[1:]
left, right := curr.Left, curr.Right
newLeft, newRight := &TreeNode{Val: val}, &TreeNode{Val: val}
curr.Left = newLeft
curr.Right = newRight
newLeft.Left = left
newRight.Right = right
}
return root
}
Complexity Analysis
Time Complexity: O(N)
Space Complexity: O(N)
